Polariton: Difference between revisions
Fabrice P. Laussy's Web
← Older editNewer edit →
Fabrice (talk | contribs)
Administrators, uploader
21,955 edits
m 1 revision imported
No edit summary
Line 3: Line 3:
The '''''Polariton''''' is a quasi-particle in condensed matter systems, where it describes the superposition of an excitation—typically an [[exciton]] (itself the quasi-particle that arises from binding a solid-state electron with a valence hole){{cite|laussy24a}}—with a photon.
The '''''Polariton''''' is a quasi-particle in condensed matter systems, where it describes the superposition of an excitation—typically an [[exciton]] (itself the quasi-particle that arises from binding a solid-state electron with a valence hole){{cite|laussy24a}}—with a photon.


The concept was first proposed theoretically, and christened, by [[John Hopfield]]{{cite|hopfield58a}}, and its most fruitful implementation, in 2D, was discovered experimentally during a sabbatical stay in [[Arakawa]]'s group in [[Tokyo]] by [[Claude Weisbuch]].{{cite|weisbuch92a}} Weisbuch did not initially recognized it as a ''Hopfield polariton'', or "bulk polariton", for which the photon is delocalized in the full 3D crystal, but as a cavity QED effect (Weisbuch was in fact already a polariton expert, having reported its first resonant observation 15 years earlier{{cite|weisbuch77a}}). The situation was quickly settled during the [[July (1993)]] Erice Summer School on "Confined Electrons and Photons: New Physics and Applications" which featured {{onlinequote|heated sessions (involving in particular the two Elis, Eli Burstein and Eli Yablonovitch) on the nature of these excitations}} according to Weisbuch himself.{{cite|weisbuch05b}} The name of "Cavity-Polariton" was then agreed to well describe Hopfield's counterpart in reduced dimensionality, and be more suitable than Weisbuch's initial choice for Rabi splitting:
The concept was first proposed theoretically, and christened so, by [[John Hopfield]]{{cite|hopfield58a}}, and its most fruitful implementation, in 2D, was discovered experimentally during a sabbatical stay in [[Arakawa]]'s group in [[Tokyo]] by [[Claude Weisbuch]],{{cite|weisbuch92a}} who referred to it as his {{onlinequote|Japanese effect.}}{{cite|houdre05a}} Weisbuch did not initially recognized it as a ''Hopfield polariton'', or "bulk polariton", for which the photon is delocalized in the full 3D crystal, but as a cavity QED effect (Weisbuch was in fact already a polariton expert, having reported its first resonant observation 15 years earlier{{cite|weisbuch77a}}). The situation was quickly settled during the [[July (1993)]] Erice Summer School on "Confined Electrons and Photons: New Physics and Applications" which featured {{onlinequote|heated sessions (involving in particular the two Elis, Eli Burstein and Eli Yablonovitch) on the nature of these excitations}} according to Weisbuch himself.{{cite|weisbuch05b}} The name of "Cavity-Polariton" was then agreed to well describe Hopfield's counterpart in reduced dimensionality, and be more suitable than Weisbuch's initial choice for merly Rabi splitting:
{{quote|The term "vacuum field Rabi splitting" has so far been used for semiconductor microcavities in analogy to atomic physics where this effect was first observed. From a solid state physics point of view, where dispersion has to be considered, the term "cavity-polariton" is more appropriate.|[[R. Houdré]], [[R.P. Stanley]] and [[U. Oesterle]]|{{weisbuch_book93a}}}}
{{quote|The term "vacuum field Rabi splitting" has so far been used for semiconductor microcavities in analogy to atomic physics where this effect was first observed. From a solid state physics point of view, where dispersion has to be considered, the term "cavity-polariton" is more appropriate.|[[R. Houdré]], [[R.P. Stanley]] and [[U. Oesterle]]|{{weisbuch_book93a}}}}
It seems that the theorists who should have predicted cavity-polaritons are [[C. Andreani]]{{etal}},{{cite|andreani91a}} who narrowly missed it by overlooking the dimensionality mismatch could be fixed with a cavity.
The first appearance of the "cavity polariton" term was in Ref. {{onlinecite|houdre94b}}, where the idea of the underlying dispersion was being formed. The breakthrough came in Ref. {{onlinecite|houdre04a}} where the now famous polariton dispersion was provided for the first time:
<center><wz tip="The first apparition of the now famous lower and upper polariton branches.">[[File:houdre94a-polariton-dispersions.jpg|360px]]</wz></center>
It seems that the theorists who should have predicted cavity-polaritons are [[C. Andreani]]{{etal}},{{cite|andreani91a}} who narrowly missed it by overlooking the dimensionality mismatch could be fixed with a cavity. He seems, however, to have readily understood (and explained) it to [[R. Houdré]]{{etal}} as they were shaping the field.{{cite|houdre05a}}
 
Historical overviews includes Refs.&nbsp;{{onlinecite|Weisbuch05b}}{{onlinecite|houdre05a}}, etc.
 
Important concepts (I'm particularly interested in) include:


* [[Polariton laser]] & [[polariton condensation]]
* [[Polariton laser]] & [[polariton condensation]]
Line 13: Line 19:
== To do ==
== To do ==


A historical review of the polariton concept, from Hopfield's lone-warrior paper{{cite|hopfield58a}} that gets all the credit despite fairly serious variations with the finally adopted results, along with other contributions.{{cite|huang51a}}{{cite|pekar57a}}
A historical review of the polariton concept, from Hopfield's lone-warrior paper{{cite|hopfield58a}} that gets all the credit despite fairly serious variations with the finally adopted results (including in its operational definition, involving four operators), along with other contributions.{{cite|huang51a}}{{cite|pekar57a}}


== Links ==
== Links ==

Revision as of 10:44, 19 August 2025

Polariton

The Polariton is a quasi-particle in condensed matter systems, where it describes the superposition of an excitation—typically an exciton (itself the quasi-particle that arises from binding a solid-state electron with a valence hole)[1]—with a photon.

The concept was first proposed theoretically, and christened so, by John Hopfield[2], and its most fruitful implementation, in 2D, was discovered experimentally during a sabbatical stay in Arakawa's group in Tokyo by Claude Weisbuch,[3] who referred to it as his «Japanese effect.»[4] Weisbuch did not initially recognized it as a Hopfield polariton, or "bulk polariton", for which the photon is delocalized in the full 3D crystal, but as a cavity QED effect (Weisbuch was in fact already a polariton expert, having reported its first resonant observation 15 years earlier[5]). The situation was quickly settled during the July (1993) Erice Summer School on "Confined Electrons and Photons: New Physics and Applications" which featured «heated sessions (involving in particular the two Elis, Eli Burstein and Eli Yablonovitch) on the nature of these excitations» according to Weisbuch himself.[6] The name of "Cavity-Polariton" was then agreed to well describe Hopfield's counterpart in reduced dimensionality, and be more suitable than Weisbuch's initial choice for merly Rabi splitting:

The term "vacuum field Rabi splitting" has so far been used for semiconductor microcavities in analogy to atomic physics where this effect was first observed. From a solid state physics point of view, where dispersion has to be considered, the term "cavity-polariton" is more appropriate.

— R. Houdré, R.P. Stanley and U. Oesterle, 🕮Confined Electrons and Photons: New Physics and Applications. Claude Weisbuch and Elias Burstein (Editors). Springer, 1995. [ISBN: 978-1-4613-5807-7]

The first appearance of the "cavity polariton" term was in Ref. [7], where the idea of the underlying dispersion was being formed. The breakthrough came in Ref. [8] where the now famous polariton dispersion was provided for the first time:

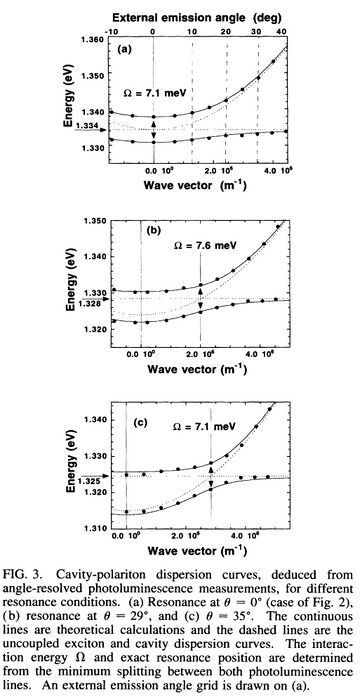
It seems that the theorists who should have predicted cavity-polaritons are C. Andreani et al.,[9] who narrowly missed it by overlooking the dimensionality mismatch could be fixed with a cavity. He seems, however, to have readily understood (and explained) it to R. Houdré et al. as they were shaping the field.[4]

Historical overviews includes Refs. [10][4], etc.

Important concepts (I'm particularly interested in) include:

To do

A historical review of the polariton concept, from Hopfield's lone-warrior paper[2] that gets all the credit despite fairly serious variations with the finally adopted results (including in its operational definition, involving four operators), along with other contributions.[11][12]

Links

References

  1. ↑ Excitons in crystals. F. P. Laussy and A. Kavokin in Encycl. Cond. Mat. Phys. 3:706 (2024). 
  2. ↑ 2.0 2.1 Theory of the Contribution of Excitons to the Complex Dielectric Constant of Crystals. J. J. Hopfield in Phys. Rev. 112:1555 (1958).
  3. ↑ Observation of the coupled exciton-photon mode splitting in a semiconductor quantum microcavity. C. Weisbuch, M. Nishioka, A. Ishikawa and Y. Arakawa in Phys. Rev. Lett. 69:3314 (1992).
  4. ↑ 4.0 4.1 4.2 Early stages of continuous wave experiments on cavity-polaritons. R. Houdré in Phys. Stat. Sol. B 242:2167 (2005).
  5. ↑ Resonant Polariton Fluorescence in Gallium Arsenide. C. Weisbuch and R. G. Ulbrich in Phys. Rev. Lett. 39:654 (1977).
  6. ↑ Microcavities in École Polytechnique Fédérale de Lausanne, École Polytechnique (France) and elsewhere: past, present and future. C. Weisbuch and H. Benisty in Phys. Stat. Sol. B 242:2345 (2005).
  7. ↑ Room-temperature cavity polaritons in a semiconductor microcavity. R. Houdré, R. P. Stanley, U. Oesterle, M. Ilegems and C. Weisbuch in Phys. Rev. B 49:16761 (1994).
  8. ↑ Template:Houdre04a
  9. ↑ Radiative lifetime of free excitons in quantum wells. L. C. Andreani, F. Tassone and F. Bassani in Solid State Commun. 77:641 (1991).
  10. ↑ Microcavities in École Polytechnique Fédérale de Lausanne, École Polytechnique (France) and elsewhere: past, present and future. C. Weisbuch and H. Benisty in Phys. Stat. Sol. B 242:2345 (2005).
  11. ↑ On the interaction between the radiation field and ionic crystals. K. Huang in Proc. R. Soc. Lond. A 208:352 (1951).
  12. ↑ Theory of electromagnetic waves in a crystal in which excitons arise. S. I. Pekar in J. Exp. Th. Phys. [ 33:1022] (1957).