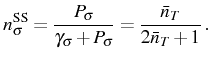The two level system: fermionic states
Excitons cannot be described in all regimes by an HO. When density is high enough to push together more than one electron or hole in the same state, the Pauli Exclusion Principle enters the picture. This is also the case of atoms, whose excitations are electronic and therefore saturable. In all these examples, the system can only populate a finite number of levels with a maximum of one excitation. The most suitable description is in terms of the projector operators:2.7
for each level (with corresponding energy
the rising (if
The free Hamiltonian of these levels is simply
Let us consider two of these levels with an energy difference of
![]() and operators of creation and destruction
and operators of creation and destruction
![]() and
and ![]() respectively. This two-level system
(2LS) covers the Fermi statistics in the same way as the HO covers
Bose statistics. Together, they describe a great deal of physical
situations, as we will see, and, most importantly, they constitute the
paradigm for the study of light-matter interaction. For what concerns
us, the 2LS is a reasonable approximation for an exciton in a small
quantum dot. The two levels involved are the ground state
respectively. This two-level system
(2LS) covers the Fermi statistics in the same way as the HO covers
Bose statistics. Together, they describe a great deal of physical
situations, as we will see, and, most importantly, they constitute the
paradigm for the study of light-matter interaction. For what concerns
us, the 2LS is a reasonable approximation for an exciton in a small
quantum dot. The two levels involved are the ground state ![]() ,
in the absence of an exciton, and the excited state
,
in the absence of an exciton, and the excited state
![]() , in its presence. The
, in its presence. The ![]() -operators
-operators
can be put in terms of the pseudo-spin operators or Pauli matrices,
used for the
summarizes the fermionic properties of the 2LS algebra. Other useful relations for normal ordering that can be derived from this algebra, are:
for
The Hamiltonian in Eq. (2.42) can be written as
A general state is described by the ![]() -dimensional density matrix. It
is characterized by two numbers: the probability of having an
excitation, which is also the average occupation
-dimensional density matrix. It
is characterized by two numbers: the probability of having an
excitation, which is also the average occupation
![]() , and the
coherence between the two levels,
, and the
coherence between the two levels,
![]() ,
,
In case of a pure state of the form
where
The maximum value that this probability can take, for infinite temperature, is
The thermal equilibrium for the mean value
![]() is
driven by the interplay of outgoing particles into the reservoir, with
a rate given by
is
driven by the interplay of outgoing particles into the reservoir, with
a rate given by
![]() (
(
![]() is the Einstein A-coefficient), and incoming
particles, at the rate
is the Einstein A-coefficient), and incoming
particles, at the rate
![]() . The incoming rate is, in contrast with the
bosonic case, proportional to the subtraction
. The incoming rate is, in contrast with the
bosonic case, proportional to the subtraction
![]() ,
which is the probability of the system being in the ground state and
therefore available for excitation. This provides the saturation
effect, as now, with the same definition for the effective parameters
as in the previous section,
,
which is the probability of the system being in the ground state and
therefore available for excitation. This provides the saturation
effect, as now, with the same definition for the effective parameters
as in the previous section,
![]() and
and
![]() (the Einstein
B-coefficient), the rate equations reads:
(the Einstein
B-coefficient), the rate equations reads:
The SS of Eq. (2.50) can be also written as
At very high temperatures, as the total income approaches the outcome,
It is interesting to note that the 2LS dynamics is symmetric under the
exchange of pump and decay (
![]() )
if we also exchange the ground and the excited states. Saturation can
occur in two senses, in the ground state when the decay is large, and
in the excited state when the pump is large. The equivalence between
pump and decay for the 2LS is in contrast with the totally different
nature that they bear in the HO, where the pump can put up to infinite
excitations (when
)
if we also exchange the ground and the excited states. Saturation can
occur in two senses, in the ground state when the decay is large, and
in the excited state when the pump is large. The equivalence between
pump and decay for the 2LS is in contrast with the totally different
nature that they bear in the HO, where the pump can put up to infinite
excitations (when
![]() ) but the decay can only
``saturate'' the system in the ground state.
) but the decay can only
``saturate'' the system in the ground state.
Elena del Valle ©2009-2010-2011-2012.


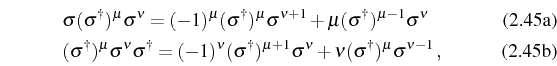
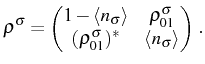
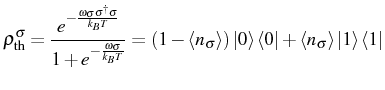
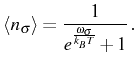
![$\displaystyle \frac{d\langle n_\sigma(t)\rangle }{dt}=-\gamma_\sigma\langle n_\sigma(t)\rangle +P_\sigma[1-\langle n_\sigma(t)\rangle ]\,.$](img275.png)