Incoherent processes: master equation and Lindblad terms
The correct description of the system dynamics must include the
decoherence processes, as we explained in
Section 2.1. The first element to take into
account is dissipation. The excitations (photons, excitons or
polaritons) will eventually leak out of the system (the cavity in our
case). Apart from the decoherence induced in the system, these
excitations can be detected from the outside and provide valuable
information of the light-matter coupling inside the cavity. Therefore,
at zero temperature--as we have seen when studying the thermal
equilibrium states--photons and excitons in the cavity have a finite
lifetime (![]() ). At
). At ![]() , not only the dissipation rate is
now given by Eq. (2.32), but also there is an
intrinsic particle income from the environment with a rate given by
Eq. (2.31). In order to take this into
account, the model is upgraded from a Hamiltonian
[Eq. 2.53)] to a Liouvillian
description with a quantum dissipative master equation for
the density matrix of the system
, not only the dissipation rate is
now given by Eq. (2.32), but also there is an
intrinsic particle income from the environment with a rate given by
Eq. (2.31). In order to take this into
account, the model is upgraded from a Hamiltonian
[Eq. 2.53)] to a Liouvillian
description with a quantum dissipative master equation for
the density matrix of the system ![]() :
:
Each superoperator
Mainly, there are two possible (and complementary) derivations of these terms in the literature. The first one is the microscopic approach described by Carmichael (2002) or Gardiner (1991). It consists in considering dissipation as a coupling to a bath of oscillators and taking the following steps:
- In the interaction picture, we apply second order perturbation theory on the coupling constants.
- Born approximation: we assume that the coupling is so weak that system and reservoir are separable at all times and that the bath is too large to be affected by the system dynamics.
- We consider a Markovian environment: the interactions with the system take place at a longer timescale than the environment's internal dynamics and, therefore, any correlations induced in the environment by such interactions are quickly lost.
- We trace out the reservoir degrees of freedom making use of their bosonic statistics in thermal equilibrium.
- We change back to the Schrödinger picture.
In this frame, the escape of the cavity photons is accounted for by
the coupling to a reservoir of exterior photons in thermal
equilibrium. The ![]() parameter is inversely proportional to the
cavity quality factor
parameter is inversely proportional to the
cavity quality factor ![]() :
:
![]() .
.
There is also the spontaneous decay of the QD into other modes than
that of the cavity, following the mechanism of Weisskopf and Wigner,
even if they are kept in the vacuum state (at zero
temperature). Although their density of states has been greatly
reduced, it will be nonzero in a realistic cavity. Nonradiative
de-excitation also takes place due to the coupling to phonons and
other particles of the solid state environment. The total QD decay
rate, ![]() , is typically much smaller than the cavity emission
rate
, is typically much smaller than the cavity emission
rate ![]() but still they can induce significant deviations from
the ideal case and should be included in an accurate description. The
environment also induces pure dephasing on the light-matter
coupling, causing the off-diagonal terms of the density matrix, linked
to light-matter coupling, to decay. I will not consider this effect
for simplicity and because in general it only contributes to destroy
the coherence, and its role is well understood.
but still they can induce significant deviations from
the ideal case and should be included in an accurate description. The
environment also induces pure dephasing on the light-matter
coupling, causing the off-diagonal terms of the density matrix, linked
to light-matter coupling, to decay. I will not consider this effect
for simplicity and because in general it only contributes to destroy
the coherence, and its role is well understood.
The last essential ingredient is the excitation of the system. In semiconductor experiments, one usually excites--optically or with electrical injection--the electronic levels far above resonance. Then, a reservoir of electron-hole pairs is created in the wetting layer with further relaxation to the exciton level. A detailed microscopic analysis of carrier capture in QDs has been developed by Nielsen et al. (2004) taking into account semiconductor many-body physics. It showed that the Coulomb scattering of electrons and holes, in delocalized states of the wetting layer, can provide efficient transitions into the discrete localized QD states. Also LO-phonons can be an important mechanism responsible for such a relaxation. Another approach with a microscopic derivation of the pumping mechanism has been recently investigated by Averkiev et al. (2009).
In this work, the pumping terms will represent only carrier capture
due to phonons, processes where a fully correlated electron-hole pair
is created in the QD. Our aim, therefore, is not to make a systematic
analysis of all the relaxation processes which are taking place in the
system. Rather, it is to develop an heuristic model where one can
investigate the impact of the pumping mechanism at a fundamental
level. The pumping is modelled by a coupling to a reservoir of
electron-hole pairs and phonons. However, some conceptual changes are
needed in the microscopic derivation of these terms that we described
above. The case of electronic pumping, for instance, is similar to the
process of laser gain: the medium requires an inversion of
electron-hole population, something that cannot be achieved by means
of a simple HO heat bath. The actual process of gaining an exciton in
the QD involves the annihilation of an electron-hole pair in an
external reservoir out of equilibrium and the emission of a phonon,
that carries the excess of energy, to another external reservoir
(which can be in thermal equilibrium). A simple effective description
of this nonequilibrium process can be made by an inverted HO with
levels
![]() maintained at a negative
temperature, as explained by Gardiner (1991). Since the
raising operator for the energy decreases the number of quanta of this
oscillator, the role of creation and destruction operators is indeed
reversed with respect to the usual case of damping. Effectively, this
results in new Lindblad terms for the incoming particles, like those
in the last term of Eq. (2.70), but that can
be controlled externally and independently. This mechanism of direct
excitation of the excitonic degree of freedom is sketched in the right
side of Fig. 2.2, where is represented the
QD under study, represented by its two levels and interacting with the
single-photonic mode with coupling strength
maintained at a negative
temperature, as explained by Gardiner (1991). Since the
raising operator for the energy decreases the number of quanta of this
oscillator, the role of creation and destruction operators is indeed
reversed with respect to the usual case of damping. Effectively, this
results in new Lindblad terms for the incoming particles, like those
in the last term of Eq. (2.70), but that can
be controlled externally and independently. This mechanism of direct
excitation of the excitonic degree of freedom is sketched in the right
side of Fig. 2.2, where is represented the
QD under study, represented by its two levels and interacting with the
single-photonic mode with coupling strength ![]() .
.
![\includegraphics[width=.6\linewidth]{chap2/fig2-schema.pdf.eps}](img358.png) |
I also consider another type of pumping, that offers a counterpart for the cavity by injecting photons incoherently. The major factor to account for such a term is the presence of many other QDs, that have been grown along with the one of interest. Those only interact weakly with the cavity. In most experimental situations so far, it is indeed difficult to find one dot with a sufficient coupling to enter the nonperturbative regime. When this is the case, all the other dots that remain in weak coupling (WC) become ``spectators'' of the strong coupling (SC) physics between the interesting dot and the cavity, and their presence is noticed by weak emission lines in the luminescence spectrum and an increased cavity emission. They are also excited by the electronic pumping that is imposed by the experimentalist, but instead of undergoing SC, they relax their energy into the cavity by Purcell enhancement or inhibition, depending on their proximity with the cavity mode. This, in turn, results in an effective pumping of the cavity as was also pointed out by Keldysh et al. (2006).
The second possible procedure to derive the Lindblad terms is based on
Monte Carlo methods and quantum jumps. In the books of
Gerry & Knight (2005) and Haroche & Raimond (2006), this approach is
preferred as it is closer to quantum information and measurement
theories. The time evolution of a system is conceived as a succession
of coherent periods of the Hamiltonian dynamics (inside a manifold)
and incoherent events (between manifolds), taking place with some
probability, which force the collapse of the wavefunction into a
given realization. In this image, the microscopic origin of the
incoherent processes is overlooked and they are just assumed to exist
with a given probability and give rise to random flows of incoming and
outcoming particles. Once we have analyzed the most relevant processes
leading to incoherent dissipation and pumping, we adopt this point of
view, as it goes better with the spirit of our study. We can define
the Liouvillian
![]() that acts in the density matrix
through the jump operator
that acts in the density matrix
through the jump operator ![]() as
as
![]() and consider the
general master equation
and consider the
general master equation
which includes the total rates for decay
It is interesting to look at the difference between the bosonic, ![]() ,
and fermionic,
,
and fermionic, ![]() , density matrices for SS of the free
particles under pump and decay. For bosons, solving the master
equation for the general term
, density matrices for SS of the free
particles under pump and decay. For bosons, solving the master
equation for the general term
![]() ,
,
leads, as we know, to the thermal mixture with average number give by Eq. (2.34):
leads to the counterpart,
In the master equation of the 2LS, we note again the equivalence
between pump and decay from the symmetry under exchange
![]() and
and
![]() . Mathematically,
this it is inherited from the simplicity of the 2LS operators,
. Mathematically,
this it is inherited from the simplicity of the 2LS operators,
![]() , that makes equivalent the Lindblad terms
for pump and decay.
, that makes equivalent the Lindblad terms
for pump and decay.
Many other Lindblad terms have been considered in the
literature. Cross terms in which both modes appear together,
![]() for instance, lead to entanglement of the modes. Such
terms can be originated from mechanisms of pump or decay that apply to
linear combinations of
for instance, lead to entanglement of the modes. Such
terms can be originated from mechanisms of pump or decay that apply to
linear combinations of ![]() and
and ![]() particles rather to the bare
modes. We will come back to this point in Chapter 3, to
discuss polariton pumping, and 6 to discuss the
joint indistinguishable pump of two identical QDs.
particles rather to the bare
modes. We will come back to this point in Chapter 3, to
discuss polariton pumping, and 6 to discuss the
joint indistinguishable pump of two identical QDs.
Other interesting Lindblad terms are those to describe incoherent
transfer of population between levels. Holland et al. (1996) used them to
describe the evaporative cooling and later Porras & Tejedor (2003) and
Laussy et al. (2004) included them in their models of polariton
condensation, in order to account for polariton-polariton and
photon-polariton scattering. It represents the scattering process of
two particles from level ![]() into another two levels 0 and
into another two levels 0 and ![]() (assuming energy and momentum conservation) when level
(assuming energy and momentum conservation) when level ![]() is
adiabatically eliminated. The jump operator describing this event is
is
adiabatically eliminated. The jump operator describing this event is
![]() . In the same way, the operator for polariton
relaxation down its dispersion, from level
. In the same way, the operator for polariton
relaxation down its dispersion, from level ![]() to 0, by phonon
emission (with energy
to 0, by phonon
emission (with energy
![]() ), is
), is
![]() . These
few-body Lindblad terms couple the modes and generate entanglement
between their populations. This results in Poissonian (coherent)
statistics for the fields even though the dynamics have a incoherent
character (see Ref. 15 in the list of my publications, in
page
. These
few-body Lindblad terms couple the modes and generate entanglement
between their populations. This results in Poissonian (coherent)
statistics for the fields even though the dynamics have a incoherent
character (see Ref. 15 in the list of my publications, in
page ![[*]](crossref.png) ).
).
Elena del Valle ©2009-2010-2011-2012.


![$\displaystyle \frac{d\rho}{dt}=i[\rho,H]+\mathcal{B}^a_T\rho+\mathcal{B}^b_T\rho\,.$](img351.png)
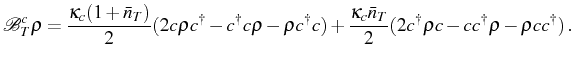
![$\displaystyle \frac{d\rho}{dt}=i[\rho,H]+\frac{\gamma_a}{2}\mathcal{L}^a\rho+\f...
...+\frac{P_a}{2}\mathcal{L}^{\ud{a}}\rho+\frac{P_b}{2}\mathcal{L}^{\ud{b}}\rho\,,$](img361.png)
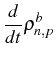
![$\displaystyle -[i \omega_b(n-p)+(\gamma+P)\frac{n+p}{2}+P]\,\rho^b_{n,p}$](img367.png)