«This clearly distinguishes polariton condensation from the

conventional lasing effect in semiconductor materials.»

Bose-Einstein Condensation of Long-Lifetime Polaritons in Thermal Equilibrium. Y. Sun, P. Wen, Y. Yoon, G. Liu, M. Steger, L. N. Pfeiffer, K. West, D. W. Snoke and K. A. Nelson in Phys. Rev. Lett. 118:016602 (2017).  What the paper says!?

This text reports polariton BEC at equilibrium, thanks to samples with a long enough lifetime to thermalize in an optical trap.

The good samples were obtained "merely" by «growing a GaAs-based high-Q microcavity structure by molecular beam epitaxy» and by making better mirrors:

The main change from samples used in previous experiments [2] was to double the number of the quarter-wavelength layers in the distributed Bragg reflectors that make up the mirrors of

the cavity;

The details (recipe & difficulties) of which are in the supplementary material. This provides them with:

The new microcavity structure has a Q of ∼320 000 and a cavity photon lifetime of ∼135 ps. This corresponds to a polariton lifetime of

270 ps at resonance.

The second ingredient is a spatial trap:

In order to guide them toward equilib- rium with a specified location and geometry, we made a spatial trap. We created an annular optical trap to localize

polaritons under nonresonant excitation.

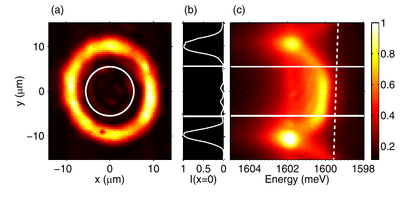
Polaritons are generated in the pump region and stream away in all directions. However, only polaritons that propagate into the center of the trap can meet and interact, leading to the accumulation of the densities high enough

for condensation.

At zero detuning (photonic-like polaritons at negative detuning thermalize less well although they still see condensation but out-of-equilibrium), they find a great agreement with the BE distribution as they increase power:

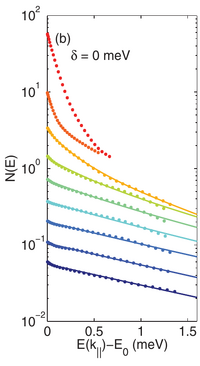
It is a bit unclear why they stop fitting beyond 1.1$P_\mathrm{BE}$ but they seem to say that the condensate peak is broadened and this, apparently, spoils their good fit:

For pump powers greater than 1.1PBE , a condensate in the ground state appears. In the weakly interacting limit, the condensate peak should be delta-function-like, which is broadened in the presence of

finite-size fluctuations [56].

That would have required more discussion, however they also point out a strong clue of genuine condensation:

The high-energy tail of the top two curves has the same absolute value, indicating that the population in the excited states saturates when there is a condensate, consistent with a Bose-Einstein condensation

phase transition for bosons in thermal equilibrium.

They call this appearance of the condensate peak "an upturn" of the distribution.

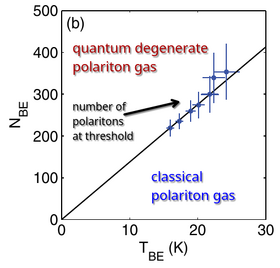
From this, they can also build «the phase diagram of polariton Bose-Einstein condensation» defined as checking the relation:

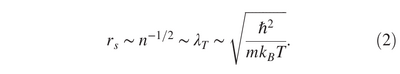
between the distance $r_s$ between excitons (obtained as the inversed density) with the thermal de Broglie wavelength $\lambda_{T}$. The inverse square of this gives a linear relationship between the number of polaritons and the temperature, which they confirm experimentally:

Criticism of previous/other works:

The upturn in the shape of N(E) in the low-energy states unambiguously distinguishes N(E) as a Bose-Einstein distribution rather than a Maxwell-Boltzmann distribution. Previous reports using short-lifetime samples [16,17] showed fits of N(E) but did not show this behavior; although a condensate peak appeared in some cases, there was not a clear density-dependent evolution from a thermal Maxwell-Boltzmann distribution to a degenerate Bose-Einstein condensed distribution. Furthermore, short- lifetime samples thermalized only when the microcavity was positively detuned [16] and the polariton character- istics were mostly excitonlike, so that the motion of the polaritons was severely restricted (see the Supplemental Material [32] for a detailed discussion). In contrast, the long-lifetime polaritons seen here at zero detuning follow Bose-Einstein statistics throughout the phase transition and

propagate to fill the trap in spatial equilibrium.

They speak of a «spectral function $A(k,\omega)$» that is easily accessible for polaritons but not for atoms.

Cites the literature suggesting BEC/superfluid departures from non-equilibrium systems as well as whether polaritons can be called BEC.

whether polariton condensates can be called Bose-Einstein condensates [27–29] [is] in part related to the question of whether polariton condensation is intrinsically a

nonequilibrium effect

Regarding no BEC in 2D:

Of course, strictly speaking, Bose-Einstein condensation (BEC) cannot occur in an ideal infinite 2D system, but it has been shown [30,31] that a 2D Bose gas in a large but finite trap has the same threshold behavior

as a 3D Bose gas in a finite trap of the same type.

Prospects of what an equilibrium polariton BEC can do:

more new experiments are possible to test theoretical predictions of interacting Bose gases which have been elusive in cold atom experiments. [such as...] excitation spectrum of the interacting Bose gas, and of the crossover from 2D to 1D equilibrium which can be controlled by spatial shaping of the excitation light to make tailored potential energy landscapes. Characteristics of the nonequilibrium state can also be studied systematically by varying the cavity detuning to control the polariton interaction strength and the excitation profile to tailor the potential landscape. Dynamical relaxation into the equilibrium state can also be studied by using pulsed rather than continuous-wave excitation followed by time-resolved measurements, as well as the coherence properties as the system passes

through the Berezinskii-Kosterlitz-Thouless transition.

Follow-up work beyond Boltzmann description include Ref..

There is an Erratum.

The paper had an accompanying Matter-Light Condensates Reach Thermal Equilibrium piece in Physics (journal) by Keeling and Marchetti, which offers little insights into the significance. In particular, while people have always complained that failure of out-of-equilibrium was problematic, now that it is demonstrated, the expert tell us that out-of-equilibrium «is not necessarily a drawback, as new physical phenomena originate from the nonequilibrium character of such condensates» and that the main result is to «show that the same system can be tuned from a highly nonequilibrium state all the way to an equilibrium state by extending the lifetime of the polaritons», overlooking the most interesting aspect which concerns the genuine aspect of BEC for polaritons, as is indeed emphasized by the Authors. K&M also make the strange comment that «As is often the case, apparently incremental progress in device fabrication and material quality leads to a transformative effect on the basic science that can be accessed.» Their discussion of the trap potential is more interesting, not only trapping but also allowing to separate the hot from cold excitons, although slightly inaccurate (the Authors don't refer to "hot" excitons). The most interesting is, however, their take on the role of interactions: