Lorentz transformations
These remarks, however, remained completely unnoticed, and a similar transformation was not again suggested until 1892 and 1895, when H. A. Lorentz published his fundamental papers on the subject.
Pauli on Voigt's 1887 transformation.
The wave equation is not Galilean invariant. It means that its form (!?)
\begin{equation} \tag{1} v^2\partial_x^2 f-\partial_t^2f=0 \end{equation}
for waves $f(x,t)$ propagating at speed $v$ in a given medium (said water) is not the same for an observer in relative motion with speed $u$ with respect to that medium.
Let us check. A Galilean transformation, as we know from the moving walkway (with speed $u$) is
\begin{align} \tag{2} x'&=x- ut\,,\\ t'&=t\,, \end{align}
where we use primes in reference to the walkway and unprimed quantities for the still ground of the airport (that for respect with the accepted terminology, we will call the laboratory frame; the 'walkway frame' is often called the 'rocket frame' or, in grievance with the relativity principle, the moving frame, which means, of course, moving relatively to the laboratory, that becomes the rest frame).
To know the effect of Eqs. ((2)) on Eq. ((1)), we need the chain rule. This states that:(!?)
\begin{align} {\partial\over \partial x}&={\partial\over\partial x'}{\partial x'\over\partial x}+{\partial\over\partial t'}{\partial t'\over\partial x}\\ {\partial\over \partial t}&={\partial\over\partial x'}{\partial x'\over\partial t}+{\partial\over\partial t'}{\partial t'\over\partial t} \end{align}
We are left with operators and derivatives of the new (walkway) variables in terms of the old (airport) ones, so we compute these:
\begin{align} {\partial x'\over\partial x}&=1\,& {\partial t'\over\partial x}&=0\\ {\partial x'\over\partial t}&=-u\,& {\partial t'\over\partial 1}&=1 \end{align}
so that, for first order derivatives, the Galilean boost yields
\begin{align} {\partial\over \partial x}&={\partial\over\partial x'}\\ {\partial\over \partial t}&=-u{\partial\over\partial x'}+{\partial\over\partial t'} \end{align}
To compute, for instance, the second-order time derivative, we do:
\begin{align} {\partial^2\over\partial t^2}&={\partial\over\partial t}{\partial\over\partial t}\\ &=\left(-u{\partial\over\partial x'}+{\partial\over\partial t'}\right)\left(-u{\partial\over\partial x'}+{\partial\over\partial t'}\right)\\ &=u^2{\partial^2\over\partial x'^2}-2u{\partial^2\over\partial x'\partial t'}+{\partial^2\over\partial t'^2} \end{align}
where we assumed commutation of the partial derivatives (remember, not always true but typically the case for well-behaved functions).
Substituting the above results in the original (airport) reference frame equation, we find:
\begin{equation} \tag{3} (v^2-u^2)\partial^2_{x'}\tilde f-\partial^2_{t'}\tilde f+2u\partial^2_{x',t'}\tilde f=0\,, \end{equation}
for $\tilde f(x',t')=f(x,t)$.
Show that the 3D wave equation transforms with a Galilean boost $\vec u$ to
\begin{equation} v^2{\nabla'}^2\tilde f-{(\vec u\cdot\nabla')^2}\tilde f-\partial^2_{t'}\tilde f+{2}\partial_{t'}\vec u\cdot \nabla'\tilde f=0\,. \end{equation}
Check that this produces the 1D result you already know when aligning your axes suitably.
The expression $v^2-u^2=(v-u)(v+u)$ gives an appealing link to how the wave equation derives from the transport equation. We know the solutions of the wave equation to be of the general form
\begin{equation} f(x,t)=\psi_+(x-vt)+\psi_-(x+vt)\,. \end{equation}
Galilean-boosting this, the solution becomes
\begin{equation} \tag{4} \tilde f(x',t')=\psi_+(x'-(v+u)t')+\psi_-(x'+(v-u)t') \end{equation}
that is, the forward propagating wave is boosted by $+u$ as it is transported along with the medium while the backward propagating one is slowed down by $-u$, going against it. Nice Galilean physics. This breaks the invariance. Not that we also get a full additional term, the cross-derivative (last term on the lhs in the equation). It is necessary for Galilean transformed waves to still be solutions, so this describes a drag term, as we can check explicitly.
So the wave equation is not Galilean invariant. If we move, we'll see different things happening. Therefore we can now if we're moving, and by how much. That is reasonable, and an intuitive picture of the world. In fact, that is how Aristotle thought things were going, as he was claiming that the Earth is still, because if it wasn't, as we throw a ball in the air, a moving Earth would catch-up distance and the ball would thus fall in the opposite direction. Since the ball falls down at the same point it is being thrown upward, this shows, says Aristotle, that the Earth is still. Galileo who had on his agenda the Heliocentric system, refuted this in a famous Dialogue (from the Dialogo sopra i due massimi sistemi del mondo) published in 1632, where he was using a canon instead and argued that the cannonball was imparted the momentum of the canon and thus was rising and falling with this component, thus showing that motion is relative. By referring to an actually slanged fall of the cannonball, Galileo revealed that he had in mind an absolute reference frame (that of the Sun, presumably). But this remained the impression of everybody until Einstein and he got the Galilean invariance correct. With this observation, this reduced or proto-version of relativity, one can consider that Physics is born.
The wave equation is not relativistic in the sense that we can detect our relative motion to it, and thus identify a favourite frame (where waves go out in all directions with the same speed, isotropically; that is the absolute, rest frame). If there is an absolute, the relative bits are secondary.
When Maxwell discovered that light is a propagation of the electromagnetic field, people looked for the medium it was propagating into. This medium, like water in the pond, would provide the absolute reference frame. This medium, yet to be identified, was called the Aether (with origins in so-called medieval science). Maxwell's equations happened to be those suitable for the Aether. Like Galileo, it was assumed the solar system was bathing in Aether and the Earth was moving through it. So by looking for changes in the speed of light in the direction of movement and opposed, or perpendicular, it was hoped one could formally get a grip on this mysterious entity.
Michelson did this experiment, together with Morley with whom he set up an interferometer, now named after them, so measure the speed of light in various direction of propagation. The setup is as follows (we refer you to your Optics Lecture to remind yourself of the details).
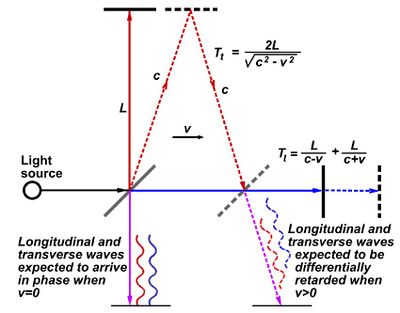
The time of flight of light transverse to propagation of motion is
\begin{equation} \tag{5} T_t=\frac{2L}{\sqrt{c^2-v^2}}\,, \end{equation}
while, along the propagation of motion, it is instead
\begin{equation} \tag{6} T_l=\frac{2L}{c^2-v^2}\,. \end{equation}
Interestingly, the times are different, so that upon recombination, the two waves are shifted, producing a translation of the interference fringes.
The first experiment [A. A. Michelson, Am. J. Sci, 122, 120 (1881)] conducted by Michelson alone, found no shift, but the resolution was harly sufficient, there was an ``extreme sensitiveness to vibration, of which, the dedicated Author later complained:
- This was so great that it was impossible to see the interference fringes except at brief intervals when working in the city, even at two o'clock in the morning.
Actually he initially made an elementary mistake when computing the distances in the Galilean frames, which was pointed out to him by an obscure science enthusiast (Alfred Poitier, it was also later raised by the more renown Lorentz). That led him to an initial over-estimation of the expected shift. Nevertheless, Michelson redid the experiment [A. A. Michelson and E. W. Morley, Am. J. Sci., 134, 333 (1887)] this time with Morley, with a much higher precision by setting the interferometer on ``a massive stone floating on mercury and ``by increasing, by repeated reflection, the path of the light to about ten times its former value. The setup as sketched by its Authors is as follows.
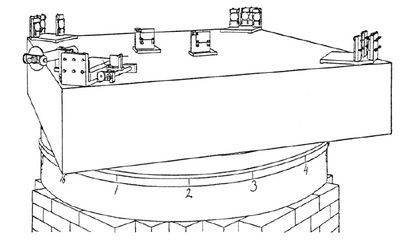
This time compellingly, they found that the relative motion of the Earth did not affect the result, unlike the prediction of Galilean Physics.
Compute the time of flight along the two branches of a Michelson interferometer that propagates with an arbitrary angle to the Aether, assuming Galilean (or conveyor belt) physics.
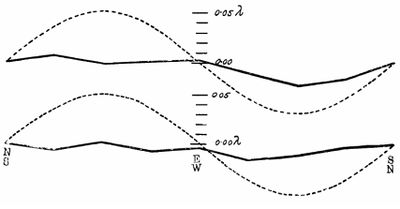
So, it seems, the speed of light is the same regardless of the relative motion of the Earth in the assumed Aether. One obvious conclusion is that Aether is not in the solar system but accompanies the planet. This is the theory of Aether drag. But this rose other difficulties (some we will discuss later on).
But let's come back to an interesting question: Newton's equations are Galilean invariant, and the wave equation applies to mechanical waves, it can be derived from Newton's mechanics, so why isn't it itself invariant? It is not because it is derived with some approximations. The exact dynamical equations for the mechanical medium, such as the continuity equation or Euler equations for fluid, are invariant under Galilean transformations. The wave equation, in contrast, is valid for small perturbations of a homogeneous non-moving background. So it is not surprising that this breaks there.
The wave equation obtained from combining Maxwell's equations, although not mechanical in origin, do not arise from known approximations. They appear to be exact. Actually, someone had the idea to ask a natural-looking question: what is the transformation that makes the wave equation invariant (the same from one set of coordinates to the other)? We know it's not Galilean. Woldemar Voigt thus tackled this and we will follow him for the while, until the point where he lost track of a major discovery, for an unfortunate (and poorly-inspired) choice of a solution but also, more importantly, a lack of physical interpretation of the equations.
The question is, mathematically, what is the change of variables of the type
\begin{align} x&=\gamma x'+\delta t'\\ t&=\epsilon x'+\zeta t' \end{align}
for four constant $\gamma$, $\delta$, $\epsilon$ and $\zeta$ to be determined such that the wave equation reads the same for $f(x,t)$ than for $\tilde f(x',t')$ to which it is equal. Note that the transformation is linear, as must be from the necessary condition that space and time have no absolute reference point. That is, it does not matter where you set zeros of space and or time, you'll find the same results. This is so obvious you might need to ponder this argument in details. At any rate, we can emphasize this by writing it as a matrix (i.e., linear) equation:
\begin{equation} \tag{7} \begin{pmatrix} x\\t \end{pmatrix}= \begin{pmatrix} \gamma &\delta\\ \epsilon&\zeta \end{pmatrix} \begin{pmatrix} x'\\t' \end{pmatrix}\,. \end{equation}
Now to carry on our program of making the wave-equation invariant, we're back to the chain rule, which we let you check gives:
Show that
\begin{align} {\partial\tilde f\over\partial x'}&=\gamma{\partial f\over\partial x}+\epsilon{\partial f\over\partial t}\\ {\partial\tilde f\over\partial t'}&=\delta{\partial f\over\partial x}+\zeta{\partial f\over\partial t}\\ {\partial^2\tilde f\over\partial x'^2}&=\gamma^2{\partial^2 f\over\partial x}+2\gamma\epsilon{\partial^2 f\over\partial x\partial t}+\epsilon^2{\partial^2 f\over\partial t^2}\\ {\partial^2\tilde f\over\partial t'^2}&=\delta^2{\partial^2 f\over\partial x}+2\delta\zeta{\partial^2 f\over\partial x\partial t}+\zeta^2{\partial^2 f\over\partial t^2} \end{align}
and, as a result, show that the wave equation, if it holds for $\tilde f$ in the $(x',t')$ reference frame under transformation (7), must satisfy:
\begin{equation} \tag{8} \partial_x^2f(\gamma^2c^2-\delta^2+\epsilon^2c^4-\zeta^2c^2)+2\partial^2_{xt}f(\gamma\epsilon c^2-\delta\zeta)=0\,. \end{equation}
For Eq. (8) to be our wave equation in the laboratory frame, it must be that:
\begin{align} c^2(\gamma^2+\epsilon^2c^2)&=\delta^2+\zeta^2c^2\\ \gamma\epsilon c^2&=\delta\zeta\tag{9} \end{align}
Two equations, four unknown, but we can remove some of them, remembering their connection to a change of reference frame. Look at the door of a gate. In the airport frame, the door doesn't move, so calling $x(t)$ its position $s$ at any time $t$, we have $dx/dt=0$. Now $dx/dt=\gamma dx'/dt+\delta dt'/dt=0$ which gives, equating it to zero
\begin{equation} {dx'\over dt'}=-{\delta\over \gamma} \end{equation}
but what is ${dx'\over dt'}$? This is the speed at which the gate door is moving from the point of view of someone on the walkway. By definition, this is $-u$, so we have:
\begin{equation} {\delta\over \gamma}=u\,. \end{equation}
Similarly, if we now look from the gate at a passenger on the conveyer belt, which stationary there (lots of people don't move on the moving walkway), we can similarly obtain the following result:
\begin{equation} {\delta\over \zeta}=u\,. \end{equation}
As a result, we have $\gamma=\zeta$. To cancel the cross-term, Eq. (9), we then also have $\epsilon=\delta/c^2$ and since $\delta=u\gamma$ we have reduced our four unknown to one, $\gamma$. Now Eq. (7) reads:
\begin{equation} \begin{pmatrix} x\\t \end{pmatrix}= \gamma \begin{pmatrix} 1&u\\ u/c^2&1 \end{pmatrix} \begin{pmatrix} x'\\t' \end{pmatrix}\,. \end{equation}
There we leave Woldemar since he made a ``wrong choice of $\gamma$ (not wrong in the mathematical sense, since this is still a possible solution, but wrong as it missed the more elegant, symmetric and meaningful choice; namely, he chose $\gamma=1$ and this is known as the Voigt transformation, that most people have never heard about). A natural choice for $\gamma$ would be the one that makes this, and the reverse transform
\begin{equation} \begin{pmatrix} x'\\t' \end{pmatrix}= {1\over \gamma}{1\over 1-u^2/c^2} \begin{pmatrix} 1&-u\\ -u/c^2&1 \end{pmatrix} \begin{pmatrix} x\\t \end{pmatrix}\,, \end{equation}
naturally symmetric, with only $u$ changing signs since, indeed, from one frame to the other we merely go in the opposite direction. That works if $\gamma$ is chosen to be
\begin{equation} \gamma={1\over\sqrt{1-u^2/c^2}}. \end{equation}
This quantity, that we will call the Lorentz factor, will be recurrent in relativity and we will keep the letter $\gamma$ to refer to it. With this choice, we now have the so-called Lorentz transformation:
\begin{align} x&={1\over\sqrt{1-u^2/c^2}}(x'+ut')\\ t&={1\over\sqrt{1-u^2/c^2}}({u\over c^2}x'+t') \end{align}
and vice-versa
\begin{align} x'&={1\over\sqrt{1-u^2/c^2}}(x-ut)\\ t'&={1\over\sqrt{1-u^2/c^2}}(-{u\over c^2}x+t)\,. \end{align}
Lorentz arrived to this result but not following this line of thought; although he knew personally Voigt, they never discussed this until Lorentz arrive to the above transformation to reconcile electromagnetism with observations. This transformation was also known from Poincaré, but both, and others, failed to bring the equations to their physical conclusions.
What would you make out of it? For Lorentz and Poincaré, it sounded as if there was a contraction of objects as they move in the Aether, maybe due to a pression of this medium against things that go through it.
This was for Einstein to make the physical breakthrough. We will discuss this in the next lectures.
Show that $u$ must be less than the speed of light and that $\gamma$ is then larger than 1. What happens when $u=c$ (moving at the same speed as the waves)? Do objects seem to contract or to expand as a result of this Lorentz factor?
Make a Taylor expansion of $\gamma$ and show that to leading order, Lorentz transform is the same as Galilean transform. Evaluate the deviations for various ratios $v/c$. Comment.
Show that a Lorentz boost (i.e., applying Lorentz transformation for the coordinates) of speed $u$ to a wave equation where waves propagate at speed $v$ yields:
\begin{equation} \frac{c^4 - u^2 v^2}{c^4-u^2 c^2} \partial^2_t\tilde{f}+2u \frac{c^4 - v^2c^2}{c^4- u^2c^2}\partial^2_{xt}\tilde{f}-c^2 \frac{v^2 c^2-u^2c^2}{c^4-u^2 c^2}\partial^2_x\tilde{f}=0 \end{equation}
What happens when $v=c$? First think on physical (relativistic) grounds, and then check.Links
- Lorentz covariance.
- https://arxiv.org/pdf/1411.2559.pdf Heras on Voigt transformation.