The principle of relativity
Nothing puzzles me more than time and space; and yet nothing troubles me less, as I never think about them.
Charles Lamb
Have you ever been in these attractions at the amusement park or pier where you are allowed to be in free fall? That doesn't last for long, but for a moment, a from a fraction of a second to a couple of them depending on the attraction, you can feel this wonderful feeling: there is no gravity.
We don't know if Einstein ever had the opportunity to experience this feeling, of which you can sometimes get a hint in a lift or on a speed bump, but he relates this feeling to the happiest thought of his life: "Because for an observer in free-fall from the roof of a house there is during the fall—at least in his immediate vicinity—no gravitational field."
So keep this feeling well in mind, and imagine yourself now in empty space, floating around (no gravity, like at this one point when the pirate's boat reverse direction). Imagine that it is also dark but that you have a flashlight, which emits pulses of light at regular intervals, with which you can signal a friend, who is somewhere else in this empty cosmos.
And sure enough, at some point, you can see their flashes of light, emitted with an identical light source as indeed the period of pulse repetitions is the same as yours. Then you also see the space station, that you just notice because it is, actually, in movement, going towards your friend. The space station is also fitted with a flashing light, although this time a different model because the period is different, it is larger, and each pulse also has a longer duration. The colour is also slightly bluer than you and your friend's lights.
You decide to also go back to the station, especially as your friend is now in, but since you are not so lucky to have it come your way, you need to thrust yourself towards it. Inspecting your spacesuit, although you notice some propellers, you don't find how to operate them. The only thing you find is one button: "home". So you click that, and slowly, very slowly, you see the station now deflects its course and comes your way. So that's it, you don't go there, it comes to you. Not the most efficient way but who cares. Soon enough, you're inside.
Once at the station itself, you notice the flashlight it is fitted with, turns outs to be, actually, the same model. It has the same repetition rate, same duration of the pulses, same colour... Why would they have changed that? Also you feel the capsule is actually more symmetric than it had seemed when you saw it at a distance, where its aspect ratio, as you remember it, was much more squeezed than it is now, that you are on its doorstep. You'd wished you would have paid more attention, which you will next time. Especially as there are a few strange things which emerge from the conversation in the ship.
Once inside, you observe how impractical it is to move everybody rather than have the spationauts come back. Nobody understands since everybody's been completely still, and everybody has clearly observed the various spationauts to make the journey back. The ship did not go towards the friend nor towards you. You both, in turn, went towards the ship. Using your propellers as operated by your on-board computer. The "home" button imparts a very slight, but continuous, acceleration of your propellers towards the ship. So you were moving, not the ship. Also, there's been no change to the flashlight on the ship. It's always been one of the unique set of many flashlights available on board.
All this is the result of one of the deepest feature of modern physics. Modern because this has been fully embraced only—relatively—recently, by Einstein, at the turn of the 20th century: the principle of relativity.
Insofar as the acceleration was not perceptible, there is no way to distinguish whether the ship was moving towards you or the other way around. The only movement that makes sense is the relative one, of both objects getting closer together. What exists is the relative distance between you and the ship. Not a background in which you, or the ship, or both, are able to move. Maybe you could have paid attention to the change and feel the acceleration and then conclude that you are the one moving. But imagine this scenario where you feel such a push towards the ship and yet the ship is going away, in the wrong direction! (because it would be itself also pushed and even more than you are in the same direction). You'd get the exact feeling of being pushed in one direction and moving in the other. So better leave the feeling aside and focus on what is observable: you getting closer or farther from the ship, without assuming either is moving. That's the principle of relativity.
It seems like a moot point. The observation with the period and duration of the flashlight shows that it's not. Just like there is no background space in which you move, there is no absolute time either that flows. Instead, so Einstein told us as he planted one pillar of modern physics, there is a new entity which merges space and time together, with the apt name of spacetime, where space and time are tightly connected. All flashlights have always been identical. But your observation of a longer period when your friend was moving in the direction of the ship, is precisely because of their relative motion. The synchronization of your flashlight with the friend means that you were not in relative motion. But both of you, in relative motion with the ship, affected your perception of time as compared to those inside the ship. For them, time was flowing normally, and their flashlight had the same period as yours for yourself. Your flashlight for them was, in fact, and/or indeed, slowed down. Because of your relative motion. How could everybody's flashlight have appeared to tick slower for every observer, as compared to their own, serving as a reference? That's an obvious contradiction.
Contradiction, no. A paradox, instead, and as a result of wrong assumptions on the nature of space and time. The paradox is resolved by spacetime and the theory of relativity. Time does not exist as an absolute, but in reference to observers in relative motion. And so does space. The different aspect ratio was also due to this relative motion. You're too small so that people in the spaceship could have noticed this, but you also were squeezed along the direction of relative motion. We assume a very large spaceship indeed for such space distortion to be visible at the high speeds involved, where such effects become predominant. Here we do not discuss, yet, optical effects and retardation and the finite speed of light, only deformation of spacetime that affect both space and time. Spacetime itself keeps some symmetry, some unity, it just stretches one component (say space) for the other (time, or vice-versa).
We are going to discuss in details such features of spacetime, its geometry and, which should help, its charting, introducing a coordinate system, or so-called reference frames. These, however, immediately bring back the underlying notion of tangible, absolute regions of space. What exists is not space bathing in time, but what we call events, namely, things that happen at a given place and a given time. Each pulse of light released by our flashlight is such an event: it occurs at the tip of our light source at the time where the photon is released. If we follow the photons, we trace a worldline in spacetime. This exists regardless of any reference frame being defined. Intersections of two worldlines define an event.
For now, we emphasize the principle of relativity, that can be stated in several different (equivalent) forms. Mermin (Space & Time in Special Relativity) gives a good account. We like this one:
- The fundamental laws of Physics are the same as observed from any inertial frame of reference.
Inertial frame of reference means one where there is no perceptible acceleration, one which, in Newtonian physics, we would say is at rest or moving at uniform velocity (there is no sense of 'rest' and uniform velocity implies a reference point, which does not exist; only events exist).
In concrete terms, there is no experiment one can do to decide whether one is in relative motion to something that is not being directly observed. If we close the Windows of the spaceshift, and it is operated so that its change of speed is not perceptible to us, then we cannot figure out whether it is in movement or not, as compared to a spationaut which we left outside and that is out of view.
That there seems to be no preferred reference frame is actually a principle as old as 'modern' physics itself, modern in the sense of its emergence from the combined use of the experimental method (Galileo) and mathematical treatment (Newton).
The Earth is about 150 million kilometres from the Sun (defined as 1AU, or one Astronomical Unit). Earth's radius is about 6400km. Those are two quantities useful to know. Using Newtonian physics, compute the average speeds at which we move through space as the result of the Earth spinning and orbiting and discuss why we don't seem to feel this as this keeps happening since we're born. This was one objection to Kepler when he proposed the heliocentric model.
While the previous distances are enough to remember approximately, one quantity is worth knowing exactly, precisely because it is exact. The speed of light $c=299\,792\,458$m/s. Combining this exact value with those above and other approximate, compute the time it takes for:
- Light to reach us from the sun.
- Light to reach us from the moon (distance Earth-moon $\approx 384\,000$km).
- Light from the sun to reach Pluto (5 billion km away).
In Space Odyssey, Earth interviews the crew aboard Discovery 1 when it's close to Jupiter. They need to edit out the waiting time for the signal to be transmitted back and forth. How much time is that?
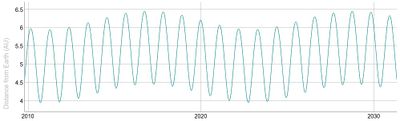
Compare with the statements made in the movie (those relevant are at the beginning, but the whole scene is interesting to see on artistic/philosophical grounds; don't trust too much the hibernation part). If they left 3 weeks ago, what is the average speed of the spaceship? How long does the interview broadcasted by the BBC (including HAL) would have taken to record? Are the questions asked in a way which supports the protocol employed?
Cray, when designing his supercomputers, was dealing with ultrafast electronics. He was delaying signals going at the speed of light in his circuits by multiples of 1ns (nanosecond, or $10^{-9}$s) by inserting cables of a given length, serving as delay lines. What length had to be these cables?
We need to specify the fundamental laws because not all laws are like this invariant to relative motion. Newton's equation are. But consider for instance waves in a pond, or so-called surface waves, as described by the wave equation:
$$\partial_t^2 f-v^2\partial_x^2 f=0$$
where $v$ is the speed of waves in the medium. If a stone is dropped, a circular ripple will be formed. Now, an observer in relative motion with the pond will observe non-circular waves, but a distortion of these, related to the so-called Doppler effect, that we will study later. Your intuition should tell you, however (and the equation confirms, next lecture) that in this case, one can infer whether one is at rest or is moving in relation to the pond, which serves as a preferred, or absolute, reference frame.
It is an experimental fact, however, that although light was identified (by Maxwell) as a wave, being indeed a solution of a wave equation as given above (for both the electric and magnetic fields), its speed was observed to be independent of any choice of a given reference frame. It was indeed assumed that light was propagating in some medium like water waves propagate in the pond. This pond for light was called the aether.
In fact, rather than this independence of the speed of light, which only came (from Michelson and Morley) at the time the solution was being formulated (by Einstein), the related phenomenon of the aberration of light was the especially puzzling feature challenging the wave theory of light. Aberration is the apparent change of the direction a light ray depending on the motion of its observer. This is a consequence of a Galilean change of reference as applied to Newtonian corpuscles, hence supporting Newton's interpretation of light. This is, however, incompatible with a Galilean boost to the wave equation, which (as we will show later) leaves the wavevector invariant.
Einstein postulated that Maxwell's equations were correct and that the wave equation which they gave rise to was valid in all reference frames, that is, with the same speed of light $c\equiv1/\sqrt{\epsilon_0\mu_0}$. This is particularly troubling because this goes against the Galilean addition of velocity, otherwise so intuitive (think of a moving walkway at the airport).
A Fields medallist is at the airport, trying to get from one end A of a very long terminal to another, B (assume the terminal is a one-dimensional line segment.) Some portions of the terminal have moving walkways (in both directions); other portions do not. His walking speed is a constant $v$, but while on a walkway, it is boosted by the speed $u$ of the walkway for a net speed of $v+u$. His objective is to get from A to B in the shortest time possible.
Suppose he needs to pause for some period of time, say to tie his shoe. Is it more efficient to do so while on a walkway, or off the walkway?
Suppose he has a limited amount of energy available to run and increase his speed to a higher quantity $v'$ (which is $v'+u$ on the walkway). Is it more efficient to run while on a walkway, or off the walkway?
This postulate has fantastic consequences for the propagation of light. It results in the strange phenomena with the flashlights which we have narrated above. In fact, beyond light, it actually, literally, affects the very notions of space and time. As such, it also leads, instead of finding a Galilean-invariant version of Maxwell's equations for electromagnetism, in replacing Newton's equations for mechanics! Relativity becomes, chiefly, a new mechanics! One can indeed pursue a Galilean version of Maxwell equations, which has some practical interest, but is a notably messy business. Interestingly, electromagnetism came to us directly in its fully-relativistic form.
Einstein's breakthrough has many consequences which are as deep as they are simple and straightforward. The speed of light becomes an instant fundamental quantity, being universal, constant and invariant (we will define all these terms, they all mean something different). It is, really, a conversion factor between space and time. It is common, in theoretical texts, to set it to one: $c=1$. We will see as well as it serves to convert mass and energy, and the most famous equation of physics
$$E=mc^2$$
which we will derive from relativistic arguments, could have been written down from mere dimensional analysis.
If space and time are, not precisely the same thing, but of a similar nature, and one can be traded for the other, with $c$ as a conversion factor, it makes sense to use the meter as a unit of time and the second as a unit of distance. Think about it. If it sounds crazy or meaningless, remember about a favourite notion from physicists for the public at large: the light-year. What is it? (a distance, a time?) Relate the light-year to the AU. What should be, then, a light-minute and a light-second? Although the terminology is not the same, what is, logically, a light-meter or a light-AU?
Using the "most famous equation of physics", how much energy can we in principle extract out of 1g of matter? (use appropriate units!) How much energy is that? What do you think were people's reaction when this became appreciated sometime between the two WW (you might have heard that Einstein wrote a letter to the US president about it).
The string of discoveries and insight does not stop here. Newton went considerably much farther than Galileo's inertial reference frame, at a constant speed. He understood that the pinnacle of Newton's theory, gravitation, was innately linked to relativity. We have seen the argument already.
Consider the trajectory of an apple thrown from the corner of the room towards the opposite wall, as shown bellow (from Taylor & Wheeler). Record its trajectory (we know from Newtonian mechanics that it is a parabola). Now consider the same experiment in the house itself in free-fall. The ball follows the same trajectory as before, but our observation in the now falling house, makes its trajectory completely different. What is it? Discuss.
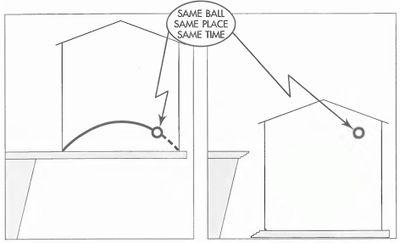
This application of the principle of relativity to accelerating frames provides a theory of gravitation, whereby the phenomenon itself is basically derived from an understanding of spacetime as having a physical reality or structure, whose dynamic is responsible for seemingly gravitational effect. This is sometimes referred to as Geometrodynamics but the universally accepted name is that of general relativity. The particular case in non-accelerating frames, in contrast, is known as special relativity (in French, relativité restreinte, i.e., in a restricted form). We will start to study the special version.
A short bibliography of relativistic texts
- David Hogg's Special relativity (see online version here). To the point, short (53 pages) exposition.