An overview of physics
What is Physics
Physics is the science of the Universe. Since it is not even clear what exactly is the "universe", in the first place (for some people, it is one's very personal perception of a wider structure known as a "multiverse", we will develop that subject in a moment), it is a science intrinsically rooted in empirical methods, approximations and abstractions.
Let us give an example. Circa 300 BC, a Macedonian bodyguard ([Somatophylakes somatophylax]) of Alexander the Great, Ptolemy, was appointed governor (satrap) of Epypt following Alexander's death. He seized power there and established himself Pharaoh, thus starting the last dynasty of ancient Egypt, the Ptolemaic dynasty, that would end with Cleopatra as a province of the Roman empire. Back at the top of the dynasty, the second ruler, Ptolemy II, was an enlightened ruler, who patronised culture and the Arts. In particular, he founded the great library of Alexandria, one of the largest and most significant libraries of the ancient world (at the bottom of the dynasty, it would be severely damaged by Cesar's invading army).

The third king of this dynasty, Ptolemy III, known as Euergetes, Benefactor, did much to develop this library. He had every book unloaded in the Alexandria docks seized and made a copy of for the library's collection. He paid considerable fines for borrowed books from the Athens library to keep them for the library instead. Most importantly, he appointed as head of this library a peculiar character, Eratosthenes, someone infatuated with knowledge and who liked to tackle problems, in particular the burning ones of the time, that were:
- Doubling the cube.
- Trisecting the angle.
- Squaring the circle.
These are mathematical problems, none of which has a solution, which was unfortunate for Eratosthenes is usually regarded as a Mathematician and one hardly gets rewarded (or famous) through failure. His main achievement in mathematics was for the sieve bearing his name to kick out non-prime numbers of a grid. Even his solution here, elegant and powerful, is not really that of a Mathematician. Eratosthenes was, actually, a Physicist, although the term didn't exist yet and would not really flesh out, incredibly, till about post second-world war. Let us now look at the main achievement of this pioneering character, which was one exploiting his geometric skill but in an altogether different context.
Eratosthenes, curious about all things, once learned of an anecdote reporting how in a southern city, then known as Syene (now Aswan), the wells would on a given day of the year, and at a given hour of this day, radiate light. Now, different people would react differently to this story. Incredulity, spiritualism, magic, curiosity, boredom... To Eratosthenes, this was possibly some combination of some of these, but the point is, he wanted to understand the reason or, as we would put it in a modern context, the "mechanism".

He had various clues for that, and needed to put them together. An important one is that the phenomenon takes place in Syene and not in Alexandria or other places. So there is something specific about this place. It would be quickly understood by many that the basic reason was that in the configuration producing the "effect", the sun was sitting right on top of the wells, finding itself somewhere along their axis, so that light is sent directly into them and is reflected back. When the sun is elsewhere, the light meets a wall before getting to the water. Eratosthenes also knew that the Earth was a sphere. This had not been proved but inferred, already from Aristotle less than a century ago, who listed several arguments for a spherical Earth: ships disappear hull first when they sail over the horizon, Earth casts a round shadow on the moon during a lunar eclipse, and different constellations are visible at different latitudes. A round-Earth, the Sun lying on a normal to a well in Syene, this starts to look like a problem of Geometry. That is the "picture" that Eratosthenes came up with:
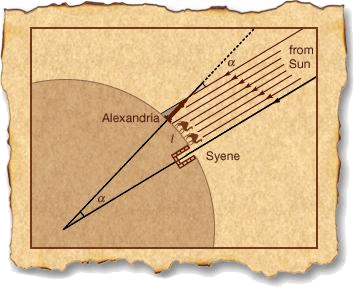
When you have drawn such a picture, you have cracked the problem. For a geometer who tried to square the circle, working out the details is a piece of cake. The insight is the vision, the understanding of how to articulate various observed phenomena to produce a model that explains them, to connect a shadow with the cosmos. And then, one of the rewarding parts of Physics, comes the applications. It is an immediate consequence of this explanation of the effect that it allows to obtain information otherwise not accessible, such as the circumference of the Earth, or, equivalently, its radius. We hear often that this was his initial intent, when it was, most probably, only a trivial consequence for free, albeit one of considerable importance. He indeed carried on to create geometry out of this insight. This is the map he got:
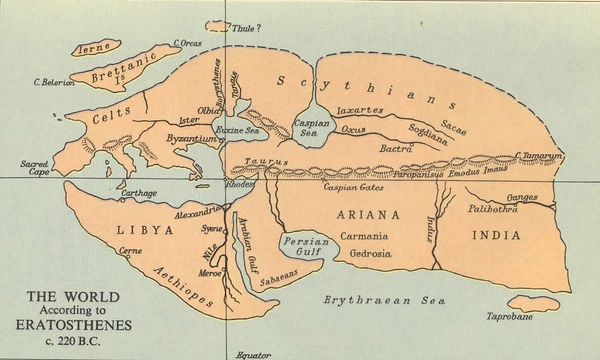
To work out the solution to the derived problem, measuring the distance, we drift into a slightly different type of science, more accurately labelled as Engineering. There are technical problems to be sorted out, such as, to measure the circumference of the Earth, one must know the distance between Alexandria and Syene. For the Physicist, an estimation would be enough. People already had a fair idea for practical purposes of the time required, that can be converted into a distance (or, equivalently, you could then obtain the circumference of the Earth in camel-time units). An Engineer, on the other hand, would want a reliable, accurate and efficient measure of this quantity. Eratosthenes, more of a Physicist than an Engineer, did not find the most brilliant solution to this one problem. It is said that he trained someone to walk with equal-step distance and had him count his footsteps from Alexandria to Syene. There are other issues to address such as synchronisation of the measurements, the angle has to be measured in Alexandria when the Sun casts no shadow in Syene. We do not know how Eratosthenes addressed this one, although as it also is an issue connected to the fundamental aspects of the problem, it is likely that Eratosthenes worked it out nicely. Indeed, assuming both cities to lie on the same meridian, which is the case in good approximation, when the Sun lies on top of the wells in Syene, it also lies at the apparent solar north (?!). This is the time at which the shadow is the shortest. So on accounts of geometry and symmetry, one can solve this problem straightforwardly. There is a fine line between Physics and Engineering. One deals with fundamental aspects, the other with technical aspects, but both otherwise addressing the same systems.
There is another fine line with the other (so-called "hard" or "exact") science that is Mathematics, that has a much more solid background in the form of axioms that serve to build an increasingly complex and unshakeable edifice.
Here is an example of what Mathematics is about: $\sqrt{2}$ is irrational.
This is related to the failure of Eratosthenes to solve the big problems of scientific Antiquity, as they were all linked ultimately to irrational numbers. More than in any other field of Science, in Mathematics, one must know what one is speaking about. Here, we involve two concepts: $\sqrt{2}$ and "irrationality". The former is a notation for the number that, multiplied by itself, is 2. The Latter means something that is not a fraction of two integers: $p/q$. The Mathematical problem is therefore to prove that for all possible $p$ and $q$, we never find that:
$$\left(\frac{p}{q}\right)^2=2\,.$$
You may want to check that you understand how we arrived to formulating the problem in this way (we applied the various definitions and brought everything together). Now we are facing a puzzle. Mathematicians are typically people who like to solve puzzles and riddles. This is one of them.
It can be solved in this way:
The numbers are such that $p^2=2q^2$. That is to say, $p^2$ is even (it is a multiple of 2: this is the definition of "even" and that is precisely what is written). Now we cannot try all the possible $p$ and $q$ but we can explore what other properties they have, until we narrow it down maybe even to their actual value. It is clear that $p$ and $q$ cannot be both even, because then they are both multiples of 2 which can be cancelled in $p/q$ so that one at most is even, or they are both odd. But the square of an even number is also even (since no factor 2 appear in a product of numbers where it is absent). Therefore, since $p^2$ is even, so is $p$, which means that $q$ is odd. But if $p$ has a factor 2, its square has a factor 4. Therefore $p^2$ can be divided by 4, i.e., $2q^2$ can be divided by four, that is, $q^2$ can be divided by 2 which means that $q^2$ is even, which means that $q$ is even. This is a contradiction, therefore there are no two integers such that $p^2=2q^2$, i.e., $\sqrt{2}$ is irrational. Quod Erat Demonstrandum.
Here we have a typical example of a Mathematical reasoning. For some people this is a headache because you have to memorize various steps and follow a tight logical thread. It is however only a question of practice and when you are used to it, this is highly enjoyable. You will notice that we used intermediate results, in fact repeatedly, such as: "if a number is even then its square is also even" and vice-versa. These can be called theorems for convenience and with a collection of theorems, like a set of keys, one can try to break the problem, like one picks a lock.
Physics, on the other hand, accumulate with much less order and structure a body of knowledge. Sometimes purely from observations. Sometimes from an insight. Some other times from underlying mathematical reasoning. This body of knowledge must remain however strongly connected to scientific methods, such as the possibility to reproduce a phenomenon so that it can be studied and verified, and therefore also can be predicted and even controlled. Questions about this phenomenon can then be asked that can be answered not from intuition or personal belief but from unarguable methods such as experimentation or experimental proof. At such Physics differs from other (so-called "soft") sciences like Philosophy or Economy or Politics, that may not be resolvable except through common agreement between different parties, what usually results in no-agreement and the parties becoming "schools" defending their own view of a problem.
Let us make a gigantic jump forward and look at a more contemporary problem, preceding the birth of quantum mechanics. This also involves shadows, this time in the spectra of light.
By 1817, Josef Fraunhofer had discovered numerous dark ’lines’, or missing wavelengths, in the solar spectrum. Subsequent investigators found many more lines - dark and bright - by applying prisms or diffraction gratings to terrestrial and celestial light sources.
At Cambridge, the chemist George Liveing and the physicist James Dewar photographed ultraviolet spectra of alkali and alkaline-earth metals. They distinguished various line series by their appearance as ’sharp’, ’principal’ or ’diffuse’ (a fourth, ’fundamental’, series was recognised in 1914). They also noticed that some groups of lines - quadruplets, triplets or pairs - reappeared at intervals. Frustratingly, though, they could not relate the frequencies of the lines in these groups to any harmonic series. It was an elderly Swiss mathematics teacher by the name of Johan Balmer who became interested in the search and applied his exceptional computational skills to the problem. In 1885 he published a formula:
There is no clear boundary between the various sciences. For instance Mathematics are greatly involved in Physics, and the field that studies their point of closest encounter is called Mathematical Physics. Philosophy also is very much involved in Physics, although unlike Mathematics, a practicing physicist can often dispense Most planetary orbits are neafrom philosophical considerations. This is illustrated by the dictum "shut up and calculate". This rather brutal injunction arose in context with one of the major branch of contemporary physics: quantum mechanics, the physics of small objects (such as particles). The science of this object led to a formulation in terms of mathematical concepts whose interpretation was not clear. Namely, a so-called "wavefunction" $\psi$ is used to describe, say, an electron, and this takes the form of a complex-valued field, a sort of "wave" (as the name implies) but really a mathematical "function" (as the name completes) since unlike a sound-wave or a water-wave, it is not known what exactly is "waving". But it is not known if this wavefunction is an actual mechanical thing or a theoretical construct that allows to recover the information on the electron such as its position or speed.
Quantum mechanics is very successful to provide calculated values for experimentally measured data, and for one of the big applications of Physics, that is, engineering, this is all that is needed: a set of rules and tricks that work. It then became largely a matter of philosophy, what exactly is the wavefunction. The most famous debates are those between Bohr and Einstein

We have given above an example of a Mathematical reasoning. Since we are dealing with Physics, we must hurry to provide a counterpart for this field. From the countless possible examples, let us consider Kepler's laws. They say how a planet orbit its star:
Mermin said it here (he remembers it here where he also shares his favorite joke, that has a bearing on our discussion:
Question: What is the difference between theoretical physics and mathematical physics?
Answer: Theoretical physics is done by physicists who lack the necessary skills to do real experiments; mathematical physics is done by mathematicians who lack the necessary skills to do real mathematics.
http://www.nature.com/news/history-shut-up-and-calculate-1.14458#/b10
Portraits of physicists:
- Galileo * Newton * Boltzmann * Noether * Feynman * Hanbury Brown * Hawking * Witten
A three-year syllabus of physics:
|
|
|