Quantum entanglement and classical behaviour. K. Molmer in J. Mod. Opt. 44:1937 (1997).  What the paper says!?

The paper argues that well-defined phases (of coherent states) are not needed (might not even exist) as entanglement produces the same results, although at the price of having to include back-action from measurements so coherent states remain interesting and useful as a mathematical formulation.

The main result is formulated by the Author as:

In this paper we demonstrate how optical interference may occur owing to an entanglement of the quantum states of light sources. We discuss classes of entangled states which are very robust against disturbances and in which the entanglement is paradoxically at the origin of classical behaviour of these systems.

Another big claim is:

One conclusion is that number state fields may yield exactly the same results as coherent fields no matter which properties one measures.

Later on:

we can predict the outcome of experiments from a statistical sampling of results based either on number states or on coherent states.

And again:

Interference effects are observed for number state fields, and the interference is related to an entanglement of the field modes monitored.

Or:

A spectacular conclusion from our simulations is that fields from thermal reservoirs can interfere. Note, however, that it is the fields transmitted through two (Fabry-Pérot) cavities (and hence frequency filtered components) that interfere.

It also claims that from this understanding, the «Heisenberg cut partly disappear(s).

The nature of this interpretation is rooted in the Hamiltonian and its most immediate consequences:

the Heisenberg equations of motion for field amplitude operators contain only atomic transition operators with essentially the same free evolution frequencies [...which...] does not rely on strict energy conservation in individual processes but rather on conservation of the number of excitations, like a superselection rule. it is relevant that operators with, for example, optical evolution frequencies couple only between themselves; hence, if they initially all have vanishing mean values, mean optical fields never develop.

Entanglement replaces coherence, and this is possible due to the form it takes:

the entanglement is quite robust against disturbances of the individual systems. The reason is that the systems are entangled in a systematic way over many number states, so that the action of an annihilation or creation operator does not change the overall form of the state vector expansion.

And:

entanglement of quantum systems may be a much more common phenomenon than commonly assumed.

And usual assumptions can be proven wrong in this setting:

entanglement is difficult to prevent, but in subsequent analyses it is often concluded that well defined phase relationships dissipate away very rapidly.

As a conclusion:

If there are no mean fields, there is no mean polarization induced in media illuminated by a light field either, and for example the classical theory of light propagation and refraction is not merely a 'theory of mean values' of the quantum theory. The optical mean field is only a convenient myth.

Zurek's pointer states are similarly seen as a convenient mathematical assumption but not the real state of affairs.

A similar (and more detailed) discussion of the idea (no phase coherence) was taken in Ref.  but here Molmer says that «{{onlinequote|this paper proceeds in a different direction}». It also relies on the realization that there is a «difficulty of producing optical fields with non-vanishing mean amplitudes.»

A lengthy discussion is also made at the end on the quite specific problem of electron-atom scattering with bichromatic lasers.

The analysis relies strongly on single-shot Monte Carlo trajectories. This clarifies a lot the problem. There is a nice juxtaposition between number and coherent states in the quantum jump approach:

The coherent state evolves continuously.

Here is a typical result of two states (from two cavities) decaying into a beam splitter and being collected by two detectors:

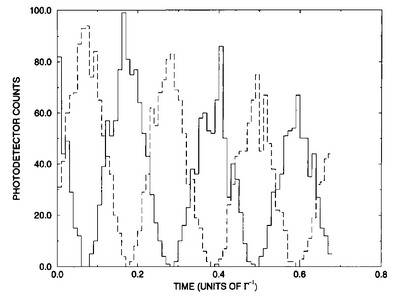
The phase is acquired randomly by spontaneous symmetry breaking in each realization. The quantity $Q\equiv\langle\ud{a}b\rangle$ captures this phenomenon at the averaged or statistical level, also with spontaneous symmetry breaking. It has a chaotic dynamics at very early times and then oscillates smoothly.

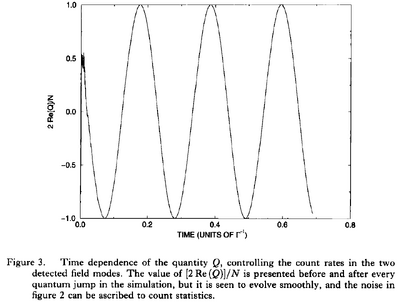
The way this is obtained is a bit unclear, being apparently the unitary dynamics between jumps from the text:

At t = 0, the quantity Q introduced in equation (15) vanishes but, after the first detection, Q $\approx$ N/4, and, during the first few jumps, Q gradually approaches the value N/2. The phase of Q at this point depends on the explicit sequence of jumps. Between jumps, equation (15) reveals a simple oscillatory behaviour of Q, which provides the harmonic variation in intensity at the two detectors.

but including several (all) the jumps from the description in the caption.

In the text, "mean field" is understood as "coherent state" (not as "mean value"):

What actually describes the system is the density matrix, not the pure state:

there is no way to distinguish experimentally between alternative pure state decompositions of the same density matrix.

Or:

Even detection records from sequences of measurements do not enable the observer to go beyond the density matrix and to identify any such thing as the ‘true’ states populated probabilistically by the system.

Points to various related works in the BEC case. I can't find the Dalibard's seminar at the 1996 Les Houches workshop titled "Collective Effects in Ultracold Atomic Gases", which does not appear to have been published, which is a pithy as perplexing comments are reproduced here. Molmer also refers «to the papers on degenerate Bose gases in this issue for further discussion» which is Volume 44, Issue 10 (1997).