HOM
The Hong-Ou-Mandel effect (HOM for short) is a quantum-optical effect of two-photon interference. It is named after Chung Ki Hong, Zhe-Yu Ou and Leonard Mandel,[1] although similar ideas appeared simultaneously from various groups[2] (some even refer to the HOM dip as the "Shih-Alley dip").
It involves two photons feeding both inputs of a beam-splitter (BS). The basic idea is that of indistinguishability: if it cannot be tracked which photon is going through which path of the beam splitter, then the amplitudes of the two photons exiting in different ports cancel and thus they are both detected together.[3] Remarkably, through "quantum erasing",[4] this indistinguishability can occur even if the photon never "see" each other, showing that the two-photon interference is not an interference of two photons![5] This was demonstrated with a day of the photons not seeing each other![6]
As a conclusion of this photon coalescence, if placing two single-photon detectors at the outputs of the beam-splitter, they will never both detect one photon each, leading to a suppression of coincidence, known as the HOM dip. The shape of this in time can be computed from the spectral shape of the photon wavepacket.[7] A beautiful demonstration is made by Jachura and Chrapkiewicz[8]:
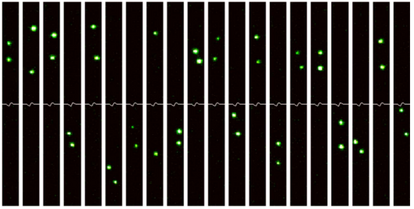
Variations include admixing a Fock state with a coherent state[9]
Classical analogue
the Hong-Ou-Mandel (HOM) effect has been referred to as “the heart of quantum mechanics” for being exquisitely quantum in nature, with absolutely no analogue in classical physics
We are particularly interested in the HOM effect with classical light, as we believe it says one thing or two about the stochastic theory of interferences (which is at the heart of the HBT effect).
The interference of classical beams was treated in detail by Pfleegor and Mandel.[10]
The theoretical limit for the HOM visibility is 1/2 for weak coherent states.[9] This was described in more detail by Chen (陈华) et al.[11]
Other cases of interest include weak coherent beams[12][13] and more generally, two-photon interferences (though not HOM) of thermal light.[14]
Testimonies
Among the whole experiments using entangled pairs of photons, the famous experiment of two-photon interference, now known as Hong-Ou-Mandel (HOM) interference [14], is probably one of the most fascinating.
References
- ↑ Measurement of subpicosecond time intervals between two photons by interference. C. K. Hong, Z. Y. Ou and L. Mandel in Phys. Rev. Lett. 59:2044 (1987).
- ↑ Two-photon interference: the Hong–Ou–Mandel effect. F. Bouchard, A. Sit, Y. Zhang, R. Fickler, F. M. Miatto, Y. Yao, F. Sciarrino and E. Karimi in Rep. Prog. Phys. 84:012402 (2020).
- ↑ Direct observation of photon pairs at a single output port of a beam-splitter interferometer. G. D. Giuseppe, M. Atatüre, M. D. Shaw, A. V. Sergienko, B. E. A. Saleh, M. C. Teich, A. J. Miller, S. W. Nam and J. Martinis in Phys. Rev. A 68:063817 (2003).
- ↑ Observation of a ‘‘quantum eraser’’: A revival of coherence in a two-photon interference experiment. P. G. Kwiat, A. M. Steinberg and R. Y. Chiao in Phys. Rev. A 45:7729 (1992).
- ↑ Can Two-Photon Interference be Considered the Interference of Two Photons?. T. B. Pittman, D. V. Strekalov, A. Migdall, M. H. Rubin, A. V. Sergienko and Y. H. Shih in Phys. Rev. Lett. 77:1917 (1996).
- ↑ Two-photon interference between continuous-wave coherent photons temporally separated by a day. D. Kim, J. Park, T. Jeong, H. Kim and H. S. Moon in Phot. Res. 8:338 (2020).
- ↑ Agata M. Brańczyk: “Hong-Ou-Mandel Interference”, 2017; arXiv:1711.00080.
- ↑ Shot-by-shot imaging of Hong–Ou–Mandel interference with an intensified sCMOS camera. M. Jachura and R. Chrapkiewicz in Opt. Lett. 40:1540 (2015).
- ↑ 9.0 9.1 Non-classical interference between independent sources. J. G. Rarity, P. R. Tapster and R. Loudon in J. Opt. B 7: (2005).
- ↑ Interference of Independent Photon Beams. R. L. Pfleegor and L. Mandel in Phys. Rev. 159:1084 (1967).
- ↑ Hong-Ou-Mandel interference with two independent weak coherent states. H. Chen, X. An, J. Wu, Z. Yin, S. Wang, W. Chen and Z. Han in Chinese Phys. B 25:020305 (2016).
- ↑ Hong–Ou–Mandel interference of two independent continuous-wave coherent photons. H. Kim, D. Kim, J. Park and H. S. Moon in Phot. Res. 8:1491 (2020).
- ↑ Two-photon interferences of weak coherent lights. H. Kim, O. Kwon and H. S Moon in Sci. Rep. 11:20555 (2021).
- ↑ Two-photon interference with thermal light. G. Scarcelli, A. Valencia and Y. Shih in Europhys. Lett. 68:618 (2004).
See also:
- Quantum theory of the lossless beam splitter. H. Fearn and R. Loudon in Opt. Commun. 64:485 (1987).
- Quantum effects in one-photon and two-photon interference. L. Mandel in Rev. Mod. Phys. 71:S274 (1999).
- Anti-Hong–Ou–Mandel interference by coherent perfect absorption of entangled photons. A. N. Vetlugin, R. Guo, C. Soci and N. I. Zheludev in New J. Phys. 24:122001 (2022).