Computación I: Projects

Now that the "theory" part of the course is complete, starts the really interesting and challenging part that embodies the principles of the University, where you get assigned your own research project. We have one project per group.

Problems

(or get them in pdf)

Random number generators

Group Beatriz Herrero Badorrey — Fco. Javier Castillo

The generation of random numbers is an important problem in several areas of computation. We will study various approaches to generate random numbers that follow arbitrary distributions. We will focus on uniform distributions of integers as far as generation is concerned and then turn to the inverse transform sampling method for distributing them accordingly. In each case, we will study the quality of randomness of our generators. We will explore simple methods such as middle-square method, linear congruential generators and others ranging from fairly elementary to, time allowing, state-of-the-art.

Celullar automata

Group Juan José García Esteban — Raúl Espinosa Copeda — Juan Ramón Deop

A cellular automaton is a set of rules applied iteratively on a finite grid, not as a numerical approximation of a field, but as an exact universe by itself. In this project, we will study the behaviour of so-called elementary cellular automata which are 1D and with two only possible states. Each cell's state is determined in time by its previous state and that of its two neighbors. We will explore such notions as complexity and universality. Then we will consider cells that can take more than two values and, in particular, consider cyclic cellular automata that exhibit behaviors of interacting particles. Time allowing, we will also study such celullar automata in 2D.

Recurrence relations

Group Maria Pilar Bueno Rodríguez — Nadia González

Recurrence relations are equations that recursively define a sequence of numbers according to simple rules, such as the Fibonacci sequence defined by $F_n=F_{n-1}+F_{n-2}$ with $F_1=F_2=1$. We will first explore a variation known as lagged Fibonacci generators, $F_n=F_{n-j}\star F_{n-k}\pmod{m}$ (with $\star$ an operation to be determined), that are popular to generate pseudo-random numbers. Then, we will explore the nonlinear relation $x_{n+1}=r x_n(1-x_n)$ for $0\le x\le 1$ and $0< r\le 4$, the so-called logistic map, that exhibits complex patterns (chaotic behavior).

Quantum computation

Group Sergio Domínguez Vidales — Alberto Castellano Mora

Quantum computation is a paradigm of computation that includes the laws of physics, in particular, quantum physics, which comes with limitations but also extensions as compared to the platonic Boolean paradigm. We will simulate a quantum computer classically, and thus explore what would be the gain of such a device if it could be implemented in a laboratory. We will start from elementary algorithms such as boson sampling, simulating simple quantum gates and, time allowing, implement more complex schemes such as the Deutsch--Jozsa algorithm or even tackle the star of quantum computation: Shor's algorithm.

Fractals in $\mathbb{C}$

Group Pablo Bastante Flores — Fernando Chacón Sánchez

Iterations of the function $f(z)=z^2+c$ of the complex number $z$ (starting from $z=0$) lead to a sequence of numbers that diverges or not. The set of points that remain bounded yields a peculiar structure, a so-called fractal set that is self-similar. We will explore this structure and some variations of it numerically. Time allowing, we will play with arbitrary precision arithmetic to go beyond machine precision and access as a remote corner as we can of the Mandelbrot set.

Volterra-Lotka equations

Group Celia de Santos Pedrazuela — David Caldevilla Asenjo

We will study the following coupled nonlinear first-order set of differential equations ($\alpha$, $\beta$, $\gamma$ and $\delta$ being real parameters):\begin{align} \frac{dx}{dt} & = \alpha x - \beta x y\,,\\ \frac{dy}{dt} & = \delta x y - \gamma y\,, \end{align}known as the Volterra-Lotka equations, that describe predator-prey interacting systems. We will study both the problem of numerical stability of various algorithms to integrate these equations and also study the dynamical stability of the trajectories of this dynamical system in the context of Stability theory. Time allowing, we will turn to more complicated dynamical systems such as the Belousov-Zhabotinsky oscillations.

Robust measures of tail weight

Group Manuel Calvo

Outliers can come to dominate completely the behaviour of a system, a phenomenon dramatized by so-called Black Swan theory. It is an important problem to characterize from empirical statistical data the behaviour of the tails of the distribution of random events, in particular to measure the impact of fat tailed distributions. We will study various proposed estimators and compare them to numerical experiments. In particular, we will investigate the distributions of the so-called kurtosis, for sums of random variables, e.g., $\sum_{i=0}^N X_i$ for $N$ Normally distributed random Variables $X_i$.

Statistical hypothesis testing

Group David Barba González — Félix Ayllón Muñoz

As much as descriptive statistics is simple and intuitive, so-called inferential statistics is subtle, complex and far-reaching. We will explore inferential statistics with numerical experiments, such as Fisher's exact test and his Lady Tasting Tea application. In particular, we will study how the bias in the estimation of the population variance is affected by Bessel's correction. We will also get acquainted with less popular distributions and in this process identify univariate distributions relationships.

Groups

The first session will be about assigning each group its project. Next session will be brainstorming and overall planning. The rest of the time will be about "cracking it".

Group Beatriz Herrero Badorrey — Fco. Javier Castillo
Group Pablo Bastante Flores — Fernando Chacón Sánchez
Group Maria Pilar Bueno Rodríguez — Nadia González
Group David Barba González — Félix Ayllón Muñoz
Group Juan José García Esteban — Raúl Espinosa Copeda — Juan Ramón Deop
Group Sergio Domínguez Vidales — Alberto Castellano Mora
Group Celia de Santos Pedrazuela — David Caldevilla Asenjo
Group Manuel Calvo

Preferences per group are as follows:

	random	cellular	recurrence	quantum	fractals	Volterra-Lotka	Tails	Inferential
Group 1	7	10	0	6	9	7	3	2
2	0	4	0	7	10	4	3	1
3	8	7	9	0	10	7	6	0
4	1	6	2	9	10	7	6	8
5	3	10	7	10	5	5	0	0
6	3	10	5	10	5	0	0	0
7	8	3	5	2	10	8	1	0
8	3	5	3	5	5	8	10	7

The average scores per problem are (out of 10):

4.125, 6.875, 3.875, 6.125, 8., 5.75, 3.625, 2.25

making Fractals highly acclaimed and statistical inference the most dreaded (little surprise in both cases). Surprisingly, however, and thankfully, every project has a high best score:

8, 10, 9, 10, 10, 8, 10, 8

The "worst best score" being 8. The corresponding min are:

0, 3, 0, 0, 5, 0, 0, 0

meaning that the "best worst score" is 5. The most wanted problem is not by everybody. Overall, we have a non-uniform group, which is good!

The average scores by group are:

5.5, 3.625, 5.875, 6.125, 5., 4.125, 4.625, 5.75

which itself has average 5.08. Several groups are basically happy with "any problem".

Problem: How to distribute the problems so that each group has a different project and optimizing everybody's preferences?

A possible answer:

We can compute the total score for all the possible permutations (there are 8!=40320) and chose one of the attributions that maximize it.

We can use, for instance the Fisher–Yates shuffle algorithm to list the permutations themselves.

The distribution of total scores is:

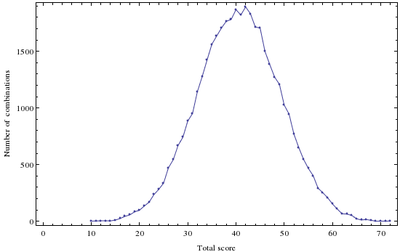
The maximum one is 72 and minimum is 10 (out of 80). Note that we are not far from the top score (73) we could have hoped for if every project got assigned to its highest score (we are a bit farther from the score where every group gets assigned their favorite project). This means that due to competition, one group got assigned a less than "worst best score" project.

There are four degenerate combinations:

1, 5, 3, 8, 2, 4, 6, 7
1, 5, 3, 8, 4, 2, 6, 7
6, 5, 3, 8, 2, 4, 1, 7
6, 5, 3, 8, 4, 2, 1, 7

which arise from groups 1 and 7, on the one hand, and 5 and 6, on the other, having expressed equal preferences (in their own vote) for the same projects.

We are thus left with:

Group 2-> Project 5

Group 3-> Project 3

Group 4-> Project 8

Group 8-> Project 7

and then, Group (1,7)->Project (1,6) and Group (5,6)->Project (2,4)

The final scores per group are:

7, 10, 9, 8, 10, 10, 8, 10

Half of the groups gets their highest rated choice, one gets their 2nd best choice. The group that gets assigned a project with the lowest collective note, below the "worst best score", is the first one (it's still 7 though, the one point missing for 73) and we can thus let them chose to lift the degeneracy.

Presentations

The presentations will take place on Monday 18th of April 2016, at the Departamento Física Teórica Materia Condensada, Modulo CV, 5th floor, in the room 01.05.SS.500.

The schedule for the morning is the following:

8:50 Doors open & Welcoming remarks