
This work explores some consequences of boson proximity, especially increased three-photon processes in the thermal phase, an idea from Kagan and Shlyapnikov.[1] This proximity is illustrated for two particles as follows (««Note that there is an enhanced probability for finding three bosons close together.»»):
They do not give details of how this was obtained or where this comes from, except from a footnote:
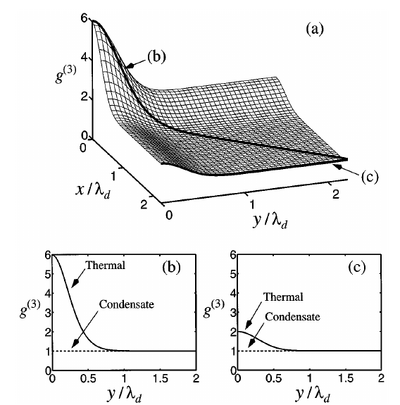
The thermal field which gives the noncondensate surface in Fig. 1 obeys Gaussian statistics with zero mean amplitude. Consequently Wick’s theorem may be iteratively applied to reduce all higher-order correlation functions to simple functionals of the first-order correlation function.
This how they comment on photon proximity and its links to quantum optics:
Note that there is an enhanced probability for finding three bosons close together. The same physics accounts for short-time photon bunching in a thermal light beam (the Hanbury-Brown-Twiss effect [10]), for the two-atom bunching that has been observed in beams of ultracold (but not condensed) atoms [11], and for three-pion correlations in pp annihilations [12,13]. To paraphrase Walls and Milburn [14] (who were in fact actually discussing two-photon correlations), the physical origin of such correlations may be understood in terms of a noisy quantum field: There is a high probability that the first boson is found at a high intensity fluctuation, and hence an enhanced probability for finding a second and third atom boson nearby.
The emphasis in their case is on two-body and three-body collisions as a way to (indirectly) evidence changes in $g^{(3)}$:
In this paper we describe collision-rate measurements that probe the higher-order coherence properties of thermal and Bose-condensed rubidium atoms. In particular, the coherence of the BEC ground state is contrasted with the chaotic fluctuations of the ultracold noncondensed states.
They reproduce the idea from Kagan and Shlyapnikov[1] in these terms:
Kagan and Shlyapnikov [16] have pointed out, however, that an easier experimental approach to probing fluctuations is to take advantage of an observable that is directly sensitive to the probability of finding three atoms near each other, that is, the loss rate of atoms due to three-body recombination. They calculated that three-body recombination in a condensate would be a factor of 3! less rapid than in a thermal cloud at the same mean density, and proposed that this change in recombination rate could be a useful signature for detecting the onset of BEC.
This is contrast to direct (or more standard) two-photon correlations, as have been performed in their Ref. [11].
Since ««The atom-bunching effect is expected to vanish in a condensate»», deviations of three-atom collisions from the phase where their proximity is magnified by 3! can be expected.
Their experiment is successful:
The central result of this paper is that our com- parison of the three-body recombination rate constant in condensed and noncondensed samples provides a quanti- tative confirmation of the predicted factor of 3! [17], and thus provides very strong evidence for the existence of higher-order coherence in Bose-condensed rubidium.
although in the foonote [17] they say that this holds for the ideal gas, and the interacting gas should not show the effect!
[17] The calculated value of 3! is for an ideal gas. Interaction- induced three-body correlations [16] lead to a correction that is smaller than the sensitivity of the present experiment.
There is also a nice analogy between atom laser & polariton BEC:
In fact, the close analogies between the macroscopically occupied state of a laser beam (characterized as a “coherent state”) and that of a Bose condensate have prompted the use of the term “atom laser” to describe some aspects of BEC [7].