The energies of the dressed states of the dissipative Jaynes-Cummings model (refer to this page for notations) read: \begin{equation} \label{eq:MonAug20130247CEST2012}
E_{\pm}^k=k\omega_a-\frac{\Delta}2-i\frac{(2k-1)\gamma_a+\gamma_\sigma}{4}
\pm\sqrt{(\sqrt{k}g)^2+\left(\frac{\Delta}2-i\frac{\gamma_a-\gamma_\sigma}4\right)^2}\,,
\end{equation}
$\Delta$ is the detuning while $\gamma_c$ (with $c=a$, $\sigma$) are the decay rates of the modes (light and matter). Everything outside of the square root refers to the bare modes. Everything inside refers to their quantum coupling. That's where, in particular, we find $g$, the coupling strength, and how it gets affected by the Jaynes-Cummings physics, namely, there is the $\sqrt{k}$ renormalization due to the light-field intensity, and the second paranthesis, $(\frac{\Delta}2-i\frac{\gamma_a-\gamma_\sigma}4)^2$, showing the combined effect of detuning and dissipation on this coupling.
The part outside the square root shows that the bare-modes physics is trivial: the states are where they are put by detuning and their lifetime is exactly the one you would put by hand (more photons means more escape). The part inside the square root is the beautiful one. Usually, dissipation is not included, as the result comes from a pure Hamiltonian picture where you get it simply by diagonalizing a matrix. This is the version with no dissipation:
\begin{equation} \label{eq:MonAug20131242CEST2012} E_{\pm}^k=k\omega_a-\frac{\Delta}2
\pm\sqrt{(\sqrt{k}g)^2+\left(\frac{\Delta}2\right)^2}\,.
\end{equation}
With the further simplification $k=1$ you get the famous anticrossing of two states. It shows that detuning helps to split the states below the square root, although this is because the bare states themselves are pushed apart by detuning in the first place.
This is the version at zero detuning:
\begin{equation}
\label{eq:MonAug20131002CEST2012}
E_{\pm}^k=k\omega_a-i\frac{(2k-1)\gamma_a+\gamma_\sigma}{4}
\pm\sqrt{(\sqrt{k}g)^2-\left(\frac{\gamma_a-\gamma_\sigma}4\right)^2}\,.
\end{equation}
This is already more interesting since the energy is now complex-valued. The real part is the energy, the imaginary part is the broadening. We see clearly that something happens when $\sqrt{k}g<(\gamma_a-\gamma_\sigma)/4$, namely, the square root goes from real to imaginary, which means that the quantum coupling doesn't shift the real part of what is outside the square root anymore but only its imaginary part, namely: the coupled-states go from splitted polaritons to the bare states again. This is the strong to weak coupling transition in the $k$th manifold of excitation.
Now, back to the full expression, Eq.~\ref{eq:MonAug20130247CEST2012}. If we expand the parenthesis, we get:
\begin{equation}
\label{eq:MonAug20130426CEST2012}
\left(\frac{\Delta}2\right)^2
-\left(\frac{\gamma_a-\gamma_\sigma}4\right)^2
-2i\frac{\gamma_a-\gamma_\sigma}4\frac{\Delta}2
\end{equation}
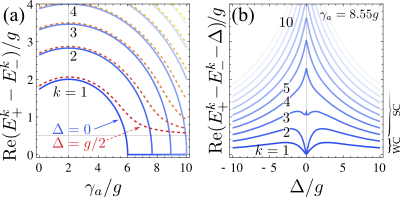
which shows that detuning keeps pushing the states apart, decay keeps bringing them closer but, there is the imaginary double product. This "additional" term has interesting consequences. One is that it shows that from the point of view of its eigenenergies, strong-coupling is really a notion well defined at resonance only. When you detune your system, you loose the clear criterion which was that polaritons collapse onto the bare states (mathematically, something real becomes imaginary). In the figure below, you see that at resonance, the blue lines that show the polaritons splitting in the various manifolds (!?) exhibit a clear transition, from a smooth circle to a flat constant (here zero). The transition is sharp and makes the curve non-differentiable at this point.You can see up to 7 in (a); you can also see that I took $\gamma_\sigma=2g$.
With detuning, however, in reddish dotted lines, this transition is smoothed out. Also, the splitting between the coupled-states never recovers that of the bare states (which in this case is at $g/2$); it only goes there asymptotically. If you plot this difference, what is done in (b), you see that it's never zero except at resonance (where the coupled-states can recover the dressed states). At any other detuning, the coupled-states are splitted farther than the bare states. In (b), we took $\gamma_a=8.55g$ so that the first two manifolds ($k=1$ and $2$) are in weak-coupling (at resonance). Indeed you see they are exactly zero for $\Delta=0$. The point is that with detuning, however, the coupled-states split away rather than following the bare states. In the 3rd rung, there is this complicated pattern where the splitting decreases with detuning (as it should for strong-coupling) but then increases again and eventually recovers the normal trend.
To summarize, strong-coupling is a notion well defined at resonance only. When the states are detuned, the concept vanishes for lack of a clear boundary and you must look for the resonance to decide. Away from it, there are even counter-intuitive results such as weakly-coupled states (defined as such at resonance) exhibiting an anomalous splitting with detuning.
We have mainly addressed the mathematical structure. This has implications in observables, to be discussed another time.