Theory of photon correlations in two-photon cascade emission. A Al-Hilfy and R Loudon in J. Phys. B.: At. Mol. Phys. 18:3697 (1985). What the paper says!?

This is a variation on the Clauser[1] experiment of photon-cascades, but using two coherent drives instead:

Much attention is paid to the violation of Cauchy inequalities. These are stronger with weak incident beams of light largely detuned from the atomic transitions.
The Hamiltonian (6) is written with quantized light-field (as if Jaynes-Cummings) which is strange as they are readily (after Eq. (16)) assumed coherent fields $\alpha_i$. They write the Bloch equations and study low and high driving regimes. They find analytical solutions (quite bulky, introducing auxiliary "fun" functions) They consider detuning.
The small-$\tau$ expansions are simple enough: ($\infty$ refers to steady-state):
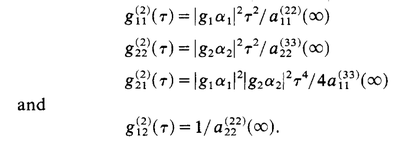
The $\tau^2$ is compatible with two cascades. Interestingly the cross-correlation is $\tau^4$. The constant in the last equation (not zero) comes from the same-cascade transition where the second photon is detected following the first one. This can be large with detuning. In the other order, this is suppressed. Due to the role of detuning, this appears to be a coherent-driving effect.
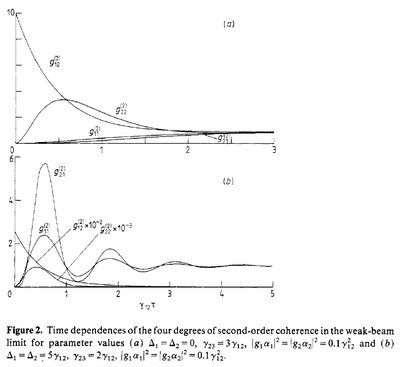
There is violation of one of the Cauchy inequalities (the upper on in Eq. (5)) at sufficiently small $\tau$ and is more pronounced at weak driving.
All-$\tau$ results are also obtained in the limits of weak and large driving. The great value of $g^{(2)}_{12}(0)$ is related to a normalization effect, with a vanishing denominator.
At high-driving, things become more symmetric, and overall less correlated, e.g., the background becomes less frequent:

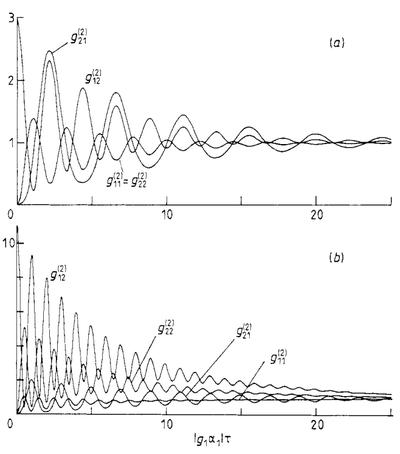
Interestingly, no comments are made on the oscillations! There is detuning at low driving and possibly dressing at high driving, but clarifications would have been useful.
Nature of the Cauchy violations:

The opening sentence already makes an interesting statement:
Experiments that measure the correlations of two readings of light intensity or photon number fall into two categories depending on whether the two intensities or photon counts to be correlated refer to a single light beam or to two different beams
Such a distinction appears unnecessary in our theory of frequency-resolved photon correlations, which sees the degenerate case as a particular one of the full spectrum of correlations.