m (→The Bohr model) |
m (→The Bohr model) |
||
| Line 13: | Line 13: | ||
$${\displaystyle {\frac{1}{\lambda}}=R_{\text{H}}\left({\frac{1}{n_{1}^{2}}}-{\frac {1}{n_{2}^{2}}}\right),}$$ | $${\displaystyle {\frac{1}{\lambda}}=R_{\text{H}}\left({\frac{1}{n_{1}^{2}}}-{\frac {1}{n_{2}^{2}}}\right),}$$ | ||
| − | with $R_\text{H}$ the Rydberg constant. [[Quantum mechanics]] first manifested itself through the efforts of [[Niels Bohr]] to find a theoretical basis for this result. The main hurdle to those who attempted such a derivation before him | + | with $R_\text{H}$ the Rydberg constant. [[Quantum mechanics]] first manifested itself through the efforts of [[Niels Bohr]] to find a theoretical basis for this result. The main hurdle to those who attempted such a derivation before him was rooted in the fact that an accelerating charge radiates, a fact well known from classical electrodynamics, which was the most successful theory of the time. Now, a circular orbit is an acceleration, not of speed (modulus) but of velocity (vector). Calculations show that the lifetime of an electron in this context is extremely short and this goes against the observed stability of hydrogen. Bohr was therefore looking for a physical picture that would constrain the motion on orbits of fixed orbits, with no possibility to spiral inward the nucleus as a result of dissipating energy. The existence of particular orbits would explain the discrete set of spectral lines. Bohr found a supporting physical picture in [[de Broglie]]'s theory of matter that states that the momentum of a particle $p$ can be related to a wave with the corresponding wavelength |
$$\lambda={h\over p}$$ | $$\lambda={h\over p}$$ | ||
| Line 35: | Line 35: | ||
$$L=n\hbar$$ | $$L=n\hbar$$ | ||
| − | for $n=1, 2, \ldots$ is called the '''principal quantum number'''. For an electron of mass $m$ and charge $e$ ( | + | for $n=1, 2, \ldots$ is called the '''principal quantum number'''. For an electron of mass $m$ and charge $-e$ (opposite as the proton so their product is $-e^2$), and moving in a circular orbit of radius $r$ in Coulomb's potential $V=-e^2/(4\pi\epsilon_0 r)$, Newton's second law $F=ma$ gives: |
| − | $${e^2\over r^2}={mv^2\over r}\label{eq:h1}$$ | + | $${e^2\over 4\pi\epsilon_0 r^2}={mv^2\over r}\label{eq:h1}$$ |
| − | since $a=v^2/r$ for a central force, with $v$ the speed of the electron. The angular momentum on the other hand is given by | + | since $a=v^2/r$ for a central force, with $v$ the speed of the electron, and $F=-|\nabla V|$. The angular momentum, on the other hand is given by |
$$L=mvr$$ | $$L=mvr$$ | ||
Revision as of 18:44, 10 March 2019
Hydrogen
Hydrogen is the most common element in the Universe. Even ourselves, being made of about 70% of water, itself consisting of 66% hydrogen (the terminology hydrogen comes from making water), we are basically hydrogen. It is therefore an important object to understand in some details.
The Bohr model
Spectroscopy in the late 19th century discovered that the radiation from hydrogen consisted of spectral lines, i.e., the emission occurs at precise frequencies.

Empirically, it was found (by Rydberg) that the lines occurred at wavelengths given by the difference of inverse square of integers:
$${\displaystyle {\frac{1}{\lambda}}=R_{\text{H}}\left({\frac{1}{n_{1}^{2}}}-{\frac {1}{n_{2}^{2}}}\right),}$$
with $R_\text{H}$ the Rydberg constant. Quantum mechanics first manifested itself through the efforts of Niels Bohr to find a theoretical basis for this result. The main hurdle to those who attempted such a derivation before him was rooted in the fact that an accelerating charge radiates, a fact well known from classical electrodynamics, which was the most successful theory of the time. Now, a circular orbit is an acceleration, not of speed (modulus) but of velocity (vector). Calculations show that the lifetime of an electron in this context is extremely short and this goes against the observed stability of hydrogen. Bohr was therefore looking for a physical picture that would constrain the motion on orbits of fixed orbits, with no possibility to spiral inward the nucleus as a result of dissipating energy. The existence of particular orbits would explain the discrete set of spectral lines. Bohr found a supporting physical picture in de Broglie's theory of matter that states that the momentum of a particle $p$ can be related to a wave with the corresponding wavelength
$$\lambda={h\over p}$$
so that, writing a condition for the orbits of the electron to corresponding to standing waves
$$2\pi r=n\lambda$$
or, equivalently, $r/\lambda=n/(2\pi)$, leads to postulating the quantization of the angular momentum $L=mvr$ (with $v$ the speed of the electron orbiting at a distance $r$ from the nucleus) into integer multiples of Planck's constant $\hbar$ (we remind that $\hbar\equiv h/(2\pi)$:
$${pr}=n{h\over2\pi}$$
where we used de Broglie's $p={h/\lambda}$. Bohr thus found out that the following postulates were enough to derive Rydberg's formula and, interestingly, link its empirically derived constant to many of the most important fundamental constants of nature:
- The electron moves in circular orbits around the atom.
- The orbit is such that the angular momentum of the electron is quantized (in units of Planck's constant $\hbar$).
- The electron can change orbits, by jumping from one to the other, releasing or acquiring the energy difference in the process.
The quantization postulate is the most important. It reads:
$$L=n\hbar$$
for $n=1, 2, \ldots$ is called the principal quantum number. For an electron of mass $m$ and charge $-e$ (opposite as the proton so their product is $-e^2$), and moving in a circular orbit of radius $r$ in Coulomb's potential $V=-e^2/(4\pi\epsilon_0 r)$, Newton's second law $F=ma$ gives:
$${e^2\over 4\pi\epsilon_0 r^2}={mv^2\over r}\tag{1}$$
since $a=v^2/r$ for a central force, with $v$ the speed of the electron, and $F=-|\nabla V|$. The angular momentum, on the other hand is given by
$$L=mvr$$
so that the Bohr quantization postulate yields:
$$mvr=n\hbar\,.\tag{2}$$
Equations (1) and (2) make two equations for two unknown $r$ and $v$, which can be easily solved:
$$\begin{align} r&=n^2a_0\,,\\ v&=\alpha c/n\,, \end{align}$$
where we have defined the Bohr radius (with units of distance):
$$\boxed{\displaystyle a_0\equiv{\hbar^2\over me^2}}$$
and the fine structure constant (which has no dimension and includes the speed of light $c$ so that $v$ can be related to a fundamental constant of speed):
$$\boxed{\displaystyle\alpha\equiv{e^2\over \hbar c}\approx{1\over 137}}$$
The measured value of the fine-structure constant is $\alpha^{−1}=137.035999173(35)$ (uncertainty in parentheses) with a great agreement to the theoretical value. The small value of this parameter is the basis for the standard model of elementary particles as it allows a perturbative treatment in terms of a series of processes whose $n$th order is weighted by $\alpha^n$. It also shows, since the speed of the electron is $v=\alpha c$, that relativistic effects can be neglected in a first approximation. If we compute the energy as kinetic $K$ (${}=\frac12mv^2$) plus potential $V$ (Coulomb), we find:
$$E={e^2\over 2r}-{e^2\over r}=-{e^2\over 2r}$$
(where we used (1) again for the kinetic energy). Substituting the radius $r$ in this results yields
$$E_n=-{mc^2\over2}{\alpha^2\over n^2}$$
or, evaluating numerically the constant:
$$E_n=-13.6\text{[eV]}{1\over n^2}\,.$$
This is an important constant that is related to Rydberg's constant and was known already at the time to be the ionization energy of Hydrogen. The 3rd Bohr postulate thus explains the discrete set of spectral lines from a transition between an initial $i$ and final state $f$ that yields an energy for the emitted photon $E_\gamma=E_i-E_f$:
$$E_\gamma=-13.6\text{[eV]}\left({1\over n_f^2}-{1\over n_i^2}\right)$$
and from Planck's formula $E_\gamma=h\nu$ relating energy and frequency, one can finally derive Rydberg's formula for the wavelengths $\lambda=c/\nu$ of the hydrogen spectrum. The underlying mechanism is thus captured in this picture:
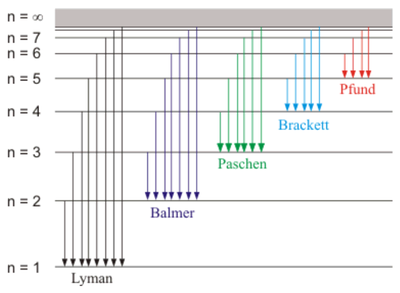
So with these simple arguments and manipulations, Bohr was clearly onto something.
Schrödinger's equation
However accurate, Bohr's model was however clearly incomplete and handwaving. In particular, although it provides correctly the energy spectrum of Hydrogen, this was