Quantum Phase of a Bose-Einstein Condensate with an Arbitrary Number of Atoms. J. Javanainen and S. M. Yoo in Phys. Rev. Lett. 76:161 (1996). What the paper says!?

This is an important paper that describes symmetry breaking from collapse of the wavefunction, what we call multiphoton symmetry breaking:
couched in statistical mechanics language, we have devised a method to investigate spontaneous symmetry breaking for a finite number of particles.
Shortly after the experimental realization of BEC, this paper explores the problem of the phase of the condensate:
it is customary to attribute to the condensate a macroscopic wave function [5,7] with a magnitude and phase.
This follows up from the earlier discovery of no-phase being needed for oscillations (ref [10] is Ref. [1])
recently, we have discovered that no phase is needed at all: The atoms will oscillate even if the condensates are initially in number states, provided the atom numbers are “large enough” [10].
In connection to which:
In this Letter we take the next, final, conceptual step. We study the interference of atoms that results when two BE condensates are dropped on top of each other.
In this text, positions of the atoms in the Fock state $\ket{N_-,N_+}$ are recorded:

where $N_\pm$ refers to atoms going in the direction $\pm k$ in a 1D system. At such it maps naturally (but without phase of the wavefunction) to our vortices.
The Authors find the $m$-body joint probability of detection for two-mode condensates flowing one against the other as:
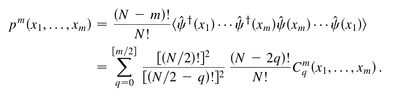
with

They also get the correspondence from one many-body reduced density matrix to another (one-particle less)—which he qualifies as "being compatible"—but without constrains on the correlators:
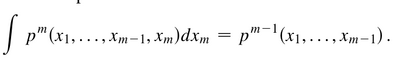
This condition, which is usually not discussed in the theory of photon detection, is crucial in order that the conventional theory of probability may be relied on.
They have a nice Monte Carlo procedure, much more efficient than ours (which is «unwise»:

From this, they get oscillations of the two condensates by multiphoton symmetry breaking:
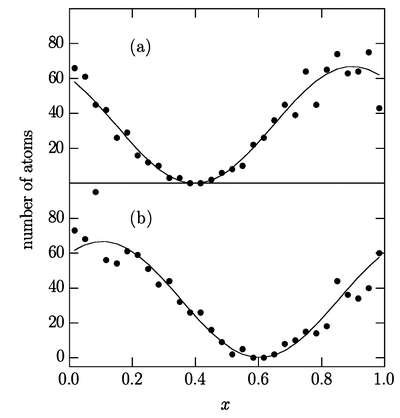
They describe the phenomenon of spontaneous symmetry breaking, without putting it by hand, but as derived from the collapse of the wavefunction:

There is no need of an external field going to zero in some (thermodynamic) limit:

Interestingly, he speaks of "mathematical fiction" (cf. K. Molmer's fictitious phase.[2])
A very interesting comment is made in a broken sentence, which points to nowhere (Ref. [12] is "S. M. Yoo et al. (unpublished)." but is probably Ref. [3]):
The question to what extent our measurement theoretical predictions and the broken-symmetry predictions can be distinguished in detail elsewhere [12].
How to separate symmetry breaking of coherent states from the multiphoton case:

There is no need of interactions!

Their result still relies heavily on correlations, as observed to single-photon imaging, as they require to let «the combining atom clouds fall on an array of position detectors».
Their concluding remark:{{This work was triggered by a question asked by W. D. Phillips: Are two light beams in number states able to interfere? Incidentally, a straightforward variant of the argument of the present paper shows that the answer is yes.}}
Here we would say, "yes, but..." (see our paper on that topic.[4])
Carmichael comments on this paper[5] as follows:
the detection of atoms in overlapping Bose-Einstein condensates produces an interference pattern ‘‘even though the condensates are taken to be in number states with no phases whatsoever’’; thus, it is not necessary for each condensate to be assigned a wave function of definite phase—specifically, for example, a coherent state.
See also
- Observation of Interference Between Two Bose Condensates. M. R. Andrews, C. G. Townsend, H. Miesner, D. S. Durfee, D. M. Kurn and W. Ketterle in Science 275:637 (1997). Experimental counterpart of the present theoretical paper.
References
- ↑ Spontaneous symmetry breaking derived from a stochastic interpretation of quantum mechanics. J. Javanainen in Phys. Lett. A 161:207 (1991).
- ↑ Optical coherence: A convenient fiction. K. Molmer in Phys. Rev. A 55:3195 (1997).
- ↑ Interference of two Bose-Einstein condensates. S. M. Yoo, J. Ruostekoski and J. Javanainen in J. Mod. Opt. 44:1763 (1997).
- ↑ Template:Guimbaogaspar25a
- ↑ Disentanglement of Source and Target and the Laser Quantum State. C. Noh and H. J. Carmichael in Phys. Rev. Lett. 100:120405 (2008).