Formation of an Exciton Polariton Condensate: Thermodynamic versus Kinetic Regimes. J. Kasprzak, D. D. Solnyshkov, R. André, Le Si Dang and G. Malpuech in Phys. Rev. Lett. 101:146404 (2008). What the paper says!?

The question of the interpretation of the recent experimental findings in terms of polariton lasing or in terms of BEC remains hot nowadays.
This work tackles the question of BEC vs laser for polariton condensation.
By combining theory (based on Boltzmann equations) and experiments, the Authors identify two key parameters—detuning and lattice temperature—that define three regimes of condensation:
- thermodynamic condensation regime (at positive detuning, with thermalization both below and above threshold, and condensation ruled by thermodynamics)
- kinetic condensation regime (at negative detuning, with no thermalization of the distribution and condensation ruled by the kinetics of relaxation)
- kinetically driven Bose condensation (in a narrow range of parameters, with a transition from a state with no temperature below threshold towards a condensed one with a temperature)
All regimes can, according to the authors, be called "polariton lasing", but "polariton BEC" is exclusive to the thermodynamic regime:
the condensate emits coherent photons and can be certainly called a polariton laser, if one is interested in fabricating a device.
The thermodynamic regime is characterized by a thermalization of polaritons at a temperature $T_\mathrm{eff}$ larger than the lattice temperature $T_\mathrm{lat}$, with which it has no time to equilibrate, but can still be in self-equilibrium with the interplay of lifetime and pumping. Given more time to thermalize, the effective temperature approaches that of the lattice and the textbook BEC is recovered, showing that dissipation in this case has a minor quantitative role.
The kinetic phase has a dynamical character with out-of-equilibrium distributions. A particular regime is identified where the system is out-of-equilibrium below threshold but at equilibrium above, what the Authors call "kinetically driven Bose condensation". Polariton interactions play a key role here as they allow to overcome the kinetic barrier thanks to stimulated scattering:
The kinetics is faster in the condensed regime because of the stimulated nature of some of the transitions, which makes the achievement of an equilibrium state easier than for an uncondensed state.
Importantly (although this is not stressed), the BEC phase is ruled by phonon-mediated relaxation, i.e., does not rely on polariton-polariton interactions, which are needed for the kinetic phase. This means that polaritons could be non-interacting and still undergo Bose-Einstein condensation, which does not rely on nonlinearities. is essentially phonon assisted (both optical and acoustic), which agrees with the picture of an equilibrium phase transition.
The paper studies both positive and negative detunings, allowing them to focus on one (thermodynamic) or the other (kinetic) regimes.
Their Fig. 2 describes the thermodynamic case at positive detunings.
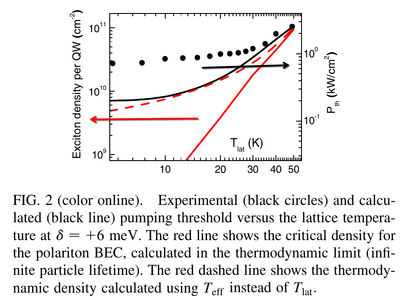
It is a confusing figure, that compares densities (red) with pumping (black), e.g., their comment where they comment on the good agreement between the red dashed and black solid lines:

They are related, but not so directly that they can be compared quantitatively.
At negative detunings, polaritons become more photon-like and relaxation is less efficient while lifetime decreases.
Their Fig. 3 describe this situation (kinetic). It lacks a reference to the threshold pumping so it is difficult to relate to the text which speaks in those terms. It shows a bottleneck with no possible fit to a Bose-Einstein distribution.
Their Fig. 4 shows the pumping threshold as a function of detuning, confirming that the best (lowest threshold) condensation is in the thermodynamic (no interaction needed) regime. It also shows that low temperatures favour condensation in the thermodynamic regime, as expected from a BEC, as opposed to the kinetic regime where higher-temperatures are better:
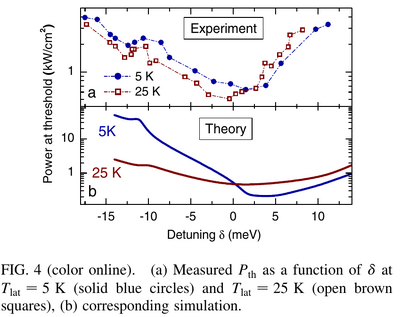
The depletion around $-13$meV is observed both in theory and experiment, and is attributed to a resonance of the exciton reservoir with optical phonons, showing that also in this kinetic regime, phonon-relaxation is important.
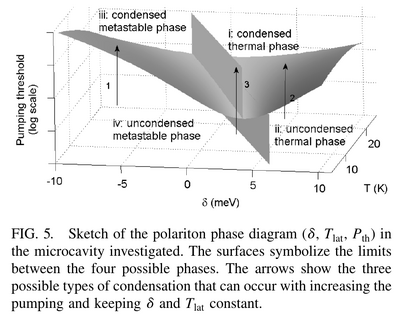
Their Fig. 5 is important but unfortunately is also confusing. The arrow 3, in particular, should go behind the upper plane.
They credit A. Ĭmamoḡlu to first propose polariton properties to make a new kind of lasers, although this is not what the paper actually says (refers to excitons instead).[1] He also tackled the polariton BEC vs lasing pictures.[2]
Distinction between laser-type sources:
- [4] G. Malpuech et al., Appl. Phys. Lett. 81, 412 (2002).
- [5] S. Chrisopoulos (sic) et al., Phys. Rev. Lett. 98, 126405 (2007).
- [6] L. V. Butov, Nature (London) 447, 540 (2007).[3]
- [7] D. Bajoni et al., Phys. Rev. Lett. 100, 047401 (2008).
and BEC-type sources:
- [8] M. Richard et al., Phys. Rev. B 72, 201301(R) (2005).
- [9] J. Kasprzak et al., Nature (London) 443, 409 (2006).
- [10] H. Deng et al., Phys. Rev. Lett. 97, 146402 (2006).
- [11] R. Balili et al., Science 316, 1007 (2007).
Arguments for Laser point of view:
- the emission of coherent photons does not require thermal equilibration within the polariton Bose gas and that the thermodynamics usually is not the driving force of the condensate formation.
Arguments for BEC point of view:
- in well-defined experimental situations, in spite of the short polariton lifetime, the relaxation kinetics can be fast enough to reach a steady state Bose distribution.
The text does not explain how the pumping threshold $P_\mathrm{th}$ is obtained theoretically. It probably is related to the occupancy in the ground state, but when dealing with a density instead of a particle number, this criterion becomes unclear (how does it depend on the sample size?)
The fit to BE distribution is not perfect above threshold, being "more condensed" in the experimental case. The Authors attribute this indeed to nonlinearities and structural disorder, although it seems to be a problem of nucleation of the condensate (the real experiment actually undergoes BEC while the numerical simulation remain with an incoherent, yet highly populated, ground state).
Their results at positive detuning (thermodynamic) are in agreement with:
- [14] H. T. Cao et al., Phys. Rev. B 69, 245325 (2004).
- [15] T. Doan et al., Solid State Commun. 145, 48 (2008).
While at negative detuning (kinetic), they are in agreement with:
- [13] D. Porras et al., Phys. Rev. B 66, 085304 (2002).