Photophysics of quantum emitters in hexagonal boron-nitride nano-flakes. M. K. Boll, I. P. Radko, A. Huck and U. L. Andersen in Opt. Express 28:7475 (2020).

They characterize four emitters (A, B, C & D) from the same sample (hBN nano-flake), using $g^{(2)}(\tau)$ as a probe of relaxation dynamics. They correlate each photon arrival event from the raw data with all the other registered photons to compute $g^{(2)}(\tau)$ instead of a histogram of time delays (start-stop method) which becomes inaccurate at long times. They thus obtain a nice series of across-timescales, self-consistently normalized data.
They find nice shapes with rounded antibunching at small times and bunching shoulders. They explain the latter with two (as opposed to usually one) shelving states. They also study blinking. This is their basic picture (their Fig. 2):
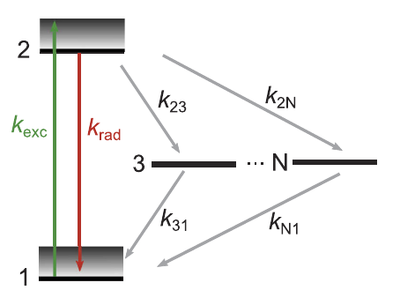
The actual ground and excited states consist of a manifold of vibrational states, as pictured. But this plays no role at room temperature.
Their rate equations connect the two shelving-states to the ground state, i.e., is not a cascade:
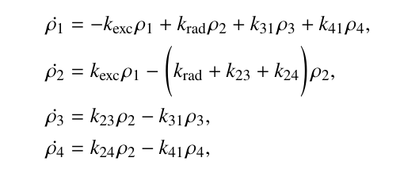
They find the need for more than one-shelving state at higher powers, but not more than two is needed. Their system is already overfitted, especially as they also include background noise.
An interesting observation is that their $g^{(2)}(\tau)$ at small times, i.e., around $\tau=0$, does not exhibit the linear $\tau$ dependence of their model (and that of similar deshelving[1]).
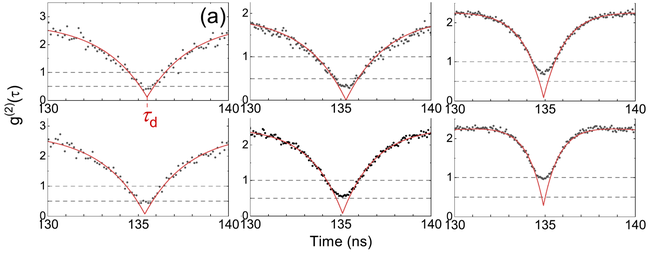
This is what they say about it:

We did not find, however, such "rounded shapes" in our analysis of how antibunching is spoilt.[2] Could it be because their shelving model misses some aspects of photon liquefaction (there is a genuine cascade somewhere)?