Latest revision as of 22:50, 12 January 2025

Qubit analog with polariton superfluid in an annular trap. J. Barrat, A. F. Tzortzakakis, M. Niu, X. Zhou, G. G. Paschos, D. Petrosyan and P. G. Savvidis in Science Advances 10:eado4042 (2024).  What the paper says!?

This work studies polariton condensates in the vortex and dipole basis. A Mexican-hat optical potential (through a SLM) makes polaritons condense in donuts with energy degeneracy. These are coupled through sample defects.

Such a control of the modes, as well as their coupling, brings the Authors to «formally identify the two polaritonic eigenmodes with the basis states of a qubit». Such a correspondence is well-known,^[1][2] but is not useful for Quantum Information Processing. The Authors escape this difficulty by referring to quantum computing without entanglement or even with classical systems (their Refs. 45‒48).

This seems to be a great experimental implementation and control of polariton condensates but the underlying theoretical picture is rather shallow. It is related to some of our works,^[3][4] which are however not cited.

Their Hamiltonian couples the two circular polarizations (also the spin-up & down along the $x$ axis):

Their canonical "qubits" are thus the horizontal ($\ket{1}$) and vertical ($\ket{0}$) dipoles.

They observe a donut (they call it "ring-shaped condensate") when the potential is symmetric, as a result of time-averaging over the Rabi oscillations between the two dipoles (their Eq. 3), which are now the eigenstates. Without coupling, they should observe a dipole, depending on the relative phase of their condensate, or a donut if condensing in one-mode only as is their case in presence of coupling.

A nearly perfectly circular trapping potential imposed by the pump laser supports a ring-shaped polariton condensate consisting of two coupled counter-rotating superfluid vortex modes

It is not entirely clear why the condensation doesn't happen in the minimum-energy state but in one vortex.

With time-resolving abilities, they would see nice dipole Rabi oscillations. They do that indirectly through autocorrelations (at the one-photon level, i.e., $g^{(1)}(\tau)$ at different points of the donut, letting them see either one mode, or the other, or their superposition:

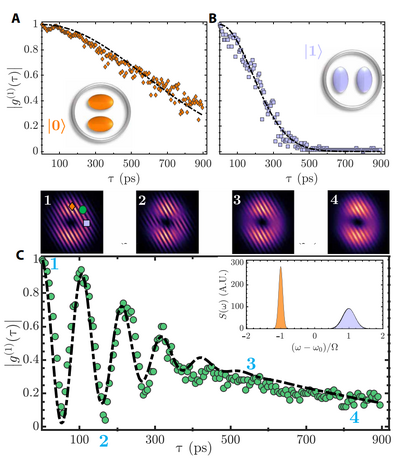
This gives them access to some interesting details of the polariton distributions (which mode is more dephased, etc.)

An interesting aspect of the work is that with a control beam, they are able to pin the condensate to a dipole (which they call "double-lobe") with a node at the control-beam position.

The main offense is their statement that «We may argue that our polaritonic system, being equivalent to a spin-1/2 in a magnetic field Ω, is a promising candidate for quantum information applications» and the planned efforts «to implement controlled interactions and gate operations between such qubits» are probably doomed to failure. However, they could flush this responsibility to other works from the literature.

They mention a "bang-bang operation" (see [1]) of which I knew nothing about.

References

1. ↑ A Classical Analogy of Entanglement. R. J. C. Spreeuw in Found. Phys. 28:361 (1998).
2. ↑ Classical wave-optics analogy of quantum-information processing. R. J. C. Spreeuw in Phys. Rev. A 63:062302 (2001).
3. ↑ Ultrafast Control and Rabi Oscillations of Polaritons. L. Dominici, D. Colas, S. Donati, J. P. Restrepo Cuartas, M. De Giorgi, D. Ballarini, G. Guirales, J. C. López Carreño, A. Bramati, G. Gigli, E. del Valle, F. P. Laussy and D. Sanvitto in Phys. Rev. Lett. 113:226401 (2014).
4. ↑ Polaritonic Rabi and Josephson oscillations. A. Rahmani and F.P. Laussy in Sci. Rep. 6:28930 (2016).