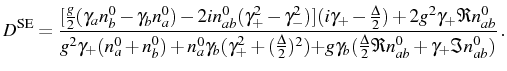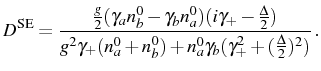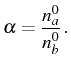Spontaneous Emission

In the case of Spontaneous Emission, where the system decays from an initial state, the boundary conditions are supplied for $\tau=0$ by the initial values $\mathbf{v}(t,t)$ , i.e., the cavity population, $n_a(t)=\langle\ud{a}a\rangle(t)$ and the coherence element $n_{ab}(t)=\langle\ud{a}b\rangle(t)$ . In turn, those are completely defined by the initial conditions, Eqs. (3.8). Although the analytical expression for these mean values as a function of time are cumbersome [see Eqs. (3.10)-(3.11)], the coefficient, Eq. (3.40), that determines quantitatively the lineshape, assumes a (relatively) simpler expression:

$\displaystyle D^\mathrm{SE}=\frac{[\frac{g}{2}(\gamma_an^0_b-\gamma_bn^0_a)-2in... ...c{\Delta}2)^2){+g\gamma_b(\frac{\Delta}2\Re n_{ab}^0+\gamma_+\Im n_{ab}^0)}}\,.$

(3.44)

To prepare the analogy with the SS case in the next section, we also write the particular case when $n_{ab}^0=0$ :

$\displaystyle D^\mathrm{SE}=\frac{\frac{g}{2}(\gamma_an^0_b-\gamma_bn^0_a)(i\ga... ...a}2)}{g^2\gamma_+(n_a^0+n_b^0)+n_a^0\gamma_b(\gamma_+^2+(\frac{\Delta}2)^2)}\,.$

(3.45)

This is an important case as it is realized whenever the initial population of one of the modes is zero, which is the typical experimental situation. Note that in this case, $D^\mathrm{SE}$ , and therefore also the normalized spectra, does not depend on the two populations independently but on their ratio only:

$\displaystyle \alpha=\frac{n_a^0}{n_b^0}\,.$

(3.46)