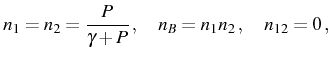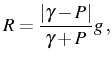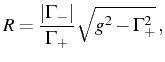Detrimentally symmetrical cases: 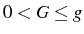
Two equal QDs create a symmetric system of levels in the
``horizontal'' sense:
![]() and
and
![]() (
(
![]() but
but
![]() ). Effectively, the populations behave as if the two
dots were uncoupled
). Effectively, the populations behave as if the two
dots were uncoupled
although the system is always in strong coupling (FSC) with
and
The second possibility is the case
![]() and
and
![]() (
(
![]() but
but
![]() ), which is symmetrical in the vertical sense. This
is equivalent to both 2LS in a thermal bath of infinite temperature,
so that pump and decay become equivalent. Now
), which is symmetrical in the vertical sense. This
is equivalent to both 2LS in a thermal bath of infinite temperature,
so that pump and decay become equivalent. Now
![]() and the
populations are also effectively uncoupled,
and the
populations are also effectively uncoupled,
![]() ,
,
![]() ,
, ![]() . The Rabi reads
. The Rabi reads
and gives the conditions for SC/WC regions in terms of
In the particular case where all the parameters are equal to ![]() ,
the symmetry is perfect in all senses (
,
the symmetry is perfect in all senses (![]() ). Again, all the levels
are equally populated (
). Again, all the levels
are equally populated (
![]() ,
, ![]() ) and uncoupled
(
) and uncoupled
(![]() ) but the Rabi vanishes. The SC/WC regimes become
conventional with
) but the Rabi vanishes. The SC/WC regimes become
conventional with
![]() . Some asymmetry in the
parameters is needed to reach the SSC and MC regimes.
. Some asymmetry in the
parameters is needed to reach the SSC and MC regimes.
Elena del Valle ©2009-2010-2011-2012.