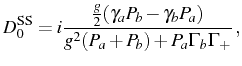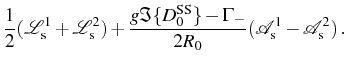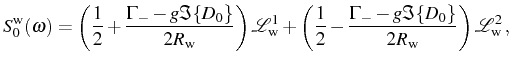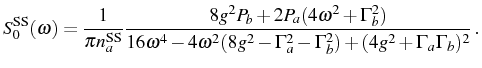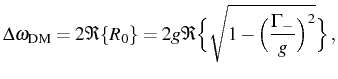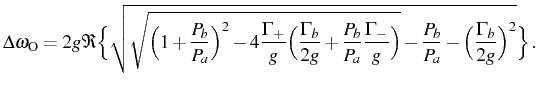Steady State under continuous incoherent pumping

In the SS, at resonance, $D_0^\mathrm{SS}$ is pure imaginary:

$\displaystyle D_0^\mathrm{SS}=i\frac{\frac{g}2(\gamma_aP_b-\gamma_bP_a)}{g^2(P_a+P_b)+P_a\Gamma_b\Gamma_+}\,,$

(3.59)

and the term that consists in the difference of Lorentzians in Eq. (3.37) disappears: $\Im\{W\}=0$ . As a result, the two peaks are equally weighted for any combination of parameters:

$\displaystyle S_0^\mathrm{SS}(\omega)=$

$\displaystyle \frac{1}{2}(\mathcal{L}_\mathrm{s}^1+\mathcal{L}_\mathrm{s}^2)+\f... ...m{SS}\}-\Gamma_{-}}{2R_0}(\mathcal{A}_\mathrm{s}^1-\mathcal{A}_\mathrm{s}^2)\,.$

(3.60)

The only way to weight more one of the peaks than the other in the SS of an incoherent pumping, would be to pump directly the polariton (dressed) states, as is the case in higher-dimensional systems were polaritons states with nonzero momentum relax into the ground state or in 0D case when cross pumping is considered. In our present model, however, such terms are excluded. The two peaks of the Rabi doublet, composed of a Lorentzian and a dispersive part, are both symmetric with respect to $\omega_a=\omega_b=0$ .

Only if $\Im\{D_0^\mathrm{SS}\}=\Gamma_{-}/g$ , the spectrum of Eq. (3.63) consists exclusively of two Lorentzians. The parameters that correspond to this case are those fulfilling either $g^2=\frac{P_a}{P_b-P_a}\Gamma_b\Gamma_{-}$ or $\Gamma_{+}=0$ . The second case corresponds to the limit of zero broadening of the upper and lower branches, that narrow as we get into a ``lasing'' region with diverging populations. Note that this spectra, composed of Lorentzians only, is the same in the exciton or photon channel of emission due to the invariance under the exchange $a\leftrightarrow b$ . In the most general case, the dispersive part will contribute to the fine quantitative structure of the spectrum, bringing closer or further apart the maxima and thus altering the apparent magnitude of the Rabi splitting. In some extreme cases, as we shall discuss, it even contrives to blur the resolution of the two peaks and a single peak results, even though the modes split in energy.

As for the weak coupling formula for the spectrum, it simplifies to:

$\displaystyle S_0^\mathrm{w}(\omega)=\left(\frac{1}{2}+ \frac{\Gamma_--g\Im\{D_... ...}-\frac{\Gamma_--g\Im\{D_0\}}{2R_\mathrm{w}}\right) \mathcal{L}_\mathrm{w}^2\,,$

(3.61)

losing completely the dispersive contribution. Both decompositions, Eqs. (3.63) and (3.64), have been given to spell-out the structure of the spectra in both regimes. The unified expression that covers them both reads explicitly:

$\displaystyle S_{0}^\mathrm{SS}(\omega)=\frac{1}{\pi n_{a}^\mathrm{SS}}\frac{8g... ...{16\omega^4-4\omega^2(8g^2-\Gamma_a^2-\Gamma_b^2)+(4g^2+\Gamma_a\Gamma_b)^2}\,.$

(3.62)

It is the counterpart for SS of Eq. (3.59), for SE. The case of excitonic emission can also be obtained, as for SE, exchanging the indexes $a\leftrightarrow b$ .

In order to study quantitatively the difference between the Rabi splitting of the dressed modes, given by

$\displaystyle \Delta \omega_\mathrm{DM} =2\Re\{R_0\}=2g\Re\Big\{\sqrt{1-\Big(\frac{\Gamma_-}{g}\Big)^2}\Big\}\,,$

(3.63)

and the observed splitting, we solve Eq. (3.52). The symmetry of the resonant spectrum regarding the central frequency $\omega_a$ allows for a solution in terms of radicals. First, $\omega_a$ is always a solution, corresponding to a minimum in the doublet case and to a maximum in the singlet case. The other two possible real solutions give rise to the desired expression for the observed splitting in the cavity spectrum, which is given, in both SC or WC, by:

$\displaystyle \Delta \omega_\mathrm{O}=2g\Re\Big\{\sqrt{\sqrt{\Big(1+\frac{P_b}... ...ac{\Gamma_-}{g}\Big)}-\frac{P_b}{P_a}-\Big(\frac{\Gamma_b}{2g}\Big)^2}\Big\}\,.$

(3.64)

This simple expression can be straight forwardly used to estimate the system parameters from the experimental resonant lineshapes or to predict the pumping rates at which the splitting will be more visible for a given configuration. The counterpart expression for the splitting observed in the direct exciton emission can be obtained by simply exchanging indexes $a\leftrightarrow b$ in Eq. (3.67).

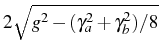The equivalent splitting in the SE emission is found by only removing $P_{a,b}$ from the $\Gamma$ 's and substituting by the ratio of initial state populations (under the assumption that initially $n_{ab}^0=0$ , which ensures a symmetric spectrum). 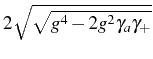In the case typically studied in the literature, that of the spontaneous emission of an excited state ( and ), we obtain the even simpler formulas $2\sqrt{g^2-(\gamma_a^2+\gamma_b^2)/8}$ and $2\sqrt{\sqrt{g^4-2g^2\gamma_a\gamma_+}}$ for the splittings in the cavity and direct exciton emission respectively, that were found by Savona & (1995) or Cui & (2006).

**Figure 3.9:** Phase space of the SS strong/weak coupling as a function of and $\gamma_a/g$ for the parameters $\gamma_b=0.1g$ and . The red lines delimit the region where there is a steady state [Eqs. (3.71)-(3.72)]. The blue line, Eq. (3.73), separates the strong (in shades of blue) from the weak (shades of red) coupling regions. The dotted black line, Eq. (3.74), separates SC and WC regions in the absence of pumping. The brown line, Eq. (3.75), separates the regions where one (dark blue) or two (light blue) peaks can be resolved in the luminescence spectra. This defines three areas in the SC region: (1) two peaks are resolved in the spectra, (2) the two peaks cannot be resolved and effectively merge into one, albeit in SC, and (3) SC is achieved thanks to the pump (with one or two peaks visible depending of the overlap with the light or dark area) despite the large dissipation that predicts WC according to Eq. (3.68). In the same way we can distinguish three regions in weak coupling: (I) standard WC, (II) SC with a two peaked spectrum and (III) WC due to pumping . The surrounding figures (a) to (e) show spectra (filled) from these regions and their decomposition into, Lorentzian (green) and dispersive (brown) parts. Parameters correspond to the points in the inset: (a) $\gamma_a=3.8g$ and , (b) $\gamma_a=3.8g$ and , (c) $\gamma_a=3.8g$ and , (d) $\gamma_a=4.49g$ and , (e) $\gamma_a=4.8g$ and . Observe how, in SC, two eigenstates have emerged, even in the cases--like in (b)--where they are not seen in the total spectrum. In the same way, in WC, all the emission emanates from the origin, although a two-peak structure can arise as a result of a resonance, also centered at the origin.
$\includegraphics[width=\linewidth]{chap3/fig9-pyramids-spectra.eps}$