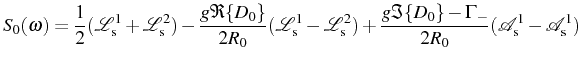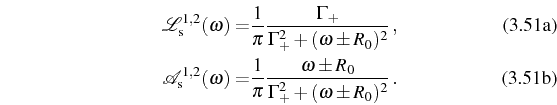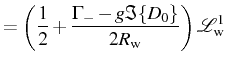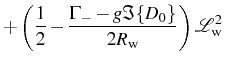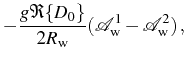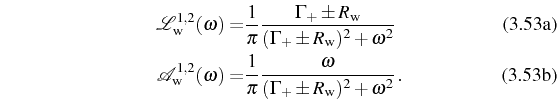Strong and Weak Coupling at resonance

Strong coupling is most marked at resonance, and this is where its signature is experimentally ascertained, in the form of an anticrossing. Fundamentally, there is another reason why resonance stands out as predominant; this is where a criterion for SC can be defined unambiguously in presence of dissipation:

WC and SC are formally defined as the regime where the complex Rabi frequency at resonance, Eq. (3.33), is pure imaginary (WC) or real (SC).

This definition, that takes into account dissipation and pumping, generalizes the classification found in the literature. The reason for this definition is mainly to be found in the behavior of the time autocorrelator, Eq. (3.29), that is respectively damped or oscillatory as a result. The exponential damping is the usual manifestation of dissipation, that decays the correlations in the field, even when a steady state is maintained. On the other hand, in the same situation of steady averages (no dynamics) but now in SC, oscillations with $\tau$ are the mark of a coherent exchange between the bare fields (the photon field and exciton field).

**Figure 3.5:** Time dynamics of the correlator $\Re\langle\ud{a}(t){a}(t+\tau)\rangle^\mathrm{SE}$ , cf. Eq. (3.29). Only the pattern of oscillations is of interest here (lighter blues correspond to higher values). In all cases, both the and $\tau$ dynamics tend to zero. Figures (a) and (b) show the SE of an exciton and of an upper polariton, respectively, in a very strongly coupled system ( $\gamma_a=0.2g$ and $\gamma_b=0.1g$ ). Fig. (c) shows the SE of an exciton in weak coupling ( $\gamma_a=5.9g$ ). The oscillations in $\tau$ , rather than in , are the mark of SC.
$\includegraphics[width=4.5cm]{chap3/newFigs/a.eps}$ $\includegraphics[width=4cm]{chap3/newFigs/b.eps}$ $\includegraphics[width=3.7cm]{chap3/newFigs/c.eps}$

**Figure 3.6:** (a) SC spectra $S_0^\mathrm{SE}(\omega)$ and (b) its corresponding mean number dynamics $n_a^\mathrm{SE}(t)$ for the SE of three different initial states: In blue solid, one exciton; in purple dashed, one photon and in brown dotted, one upper polariton. Parameters are $\gamma_a=1.9g$ and $\gamma_b=0.1g$ . Inset of (b) is the same in log-scale.
$\includegraphics[width=0.45\linewidth]{chap3/fig6a-Init-spectra-ga_1.9-gb_0.1.eps}$ $\includegraphics[width=0.45\linewidth]{chap3/fig6b-Init-dynamicsNa-ga_1.9-gb_0.1.eps}$

**Figure 3.7:** (a)-(b) Weak-coupling spectra $S_0^\mathrm{SE}(\omega)$ and (c) its corresponding mean number dynamics $n_a^\mathrm{SE}(t)$ for the SE of an exciton (a) and a photon (b) as the initial condition. In all figures, solid blue corresponds to the decay of an exciton; dashed purple to the decay of a photon and dotted brown to the decay of an upper polariton. For comparison, we plotted in (a) and (b), with solid black lines, the very different bare emission () of an exciton and photon respectively. Also in (a), in dashed black, that of an exciton decaying with the Purcell rate $\gamma_b^\mathrm{P}=4g^2/\gamma_a$ . Parameters are $\gamma_a=1.9g$ and $\gamma_b=0.1g$ . Inset of (c) is the same in log-scale.
$\includegraphics[width=0.55\linewidth]{chap3/fig7a-Exciton-Init-spectra-ga_5.9-gb_0.1.eps}$ $\includegraphics[width=0.55\linewidth]{chap3/fig7b-Photon-Init-spectra-ga_5.9-gb_0.1.eps}$ $\includegraphics[width=0.55\linewidth]{chap3/fig7c-Init-dynamicsNa-ga_5.9-gb_0.1.eps}$

In the literature, one sometimes encounters the confusion that SC is linked to a periodic transfer of energy or of population between the photon and exciton field, or that it follows from a chain of emissions and absorptions. This is an incorrect general association as one can explicit cases with apparent oscillations of populations that correspond to weak coupling, or on the contrary, cases with no oscillations of populations that are in SC. The two concepts are therefore logically unrelated in the sense that none implies the other. This is illustrated for the SE case in Figs. 3.5(a), 3.5(b) and 3.6 on the one hand, where the system is in SC, and in Fig. 3.5(c) and 3.7 on the other hand, where it is in WC. In SS, there is no dynamics in any case, so oscillations of populations are clearly unrelated to weak or strong coupling. In SE, the distinction is clearly seen in Fig. 3.5 where both the and $\tau$ dynamics are shown in a contour-plot in the case where the system is initially prepared as an exciton, (a) and (c), or as a polariton, (b). In the polariton case, the dynamics in is simply decaying (because of the lifetime), while it is clearly oscillating in $\tau$ , were the proper manifestation of SC is to be found. The decay is not exactly exponential because in the presence of dissipation, the polariton is not anymore an ideal eigenstate (the larger the dissipation, the more the departure). However this effect in SC is so small that it only consists in a small ``wobbling'' of the $\tau$ contour lines. On the other hand, the exciton, (a), that is not an eigenstate, features oscillations both in the dynamics (the one often but unduly regarded as the signature of SC), as well as the $\tau$ dynamics. In stark contrast, the exciton in WC, (c), bounces with . This, that might appear as an oscillation, is not, as it happens only once and is damped in the long-time values. This behavior is shown quantitatively in Fig. 3.6 for SC and Fig. 3.7 for WC, where the population is displayed for the SE of an exciton (blue solid), a photon (purple dashed) and an upper polariton (brown dotted), respectively, along with the luminescence spectrum that they produce (detected in the cavity emission). Here it is better seen how, for instance, the polariton-decay is wobbling as a result of the dissipation, that perturbs its eigenstate-character and leaks some population to the lower polariton. More importantly, note how very different the spectra are, depending on whether the initial state is a photon or an exciton, despite the fact that the dynamics is similar in both cases (see the inset in log-scale of their respective populations). The PL spectrum observed in the cavity emission is much better resolved when the system is initially in a photon state, than it is when the system is initially in an exciton state. The splitting is larger and the overlap of the peaks smaller in the former case. This will find an important counterpart in the SS case. In Fig. 3.7, the corresponding case of WC is shown for clarity, with a decay of populations and possible oscillations.

**Figure 3.8:** Dynamics of $\lim_{t\rightarrow\infty}\langle\ud{a}(t){a}(t+\tau)\rangle/n_a^\mathrm{SS}$ , Eq. (3.29) and (3.15a), for the SS corresponding to the points (a)-(e) in Fig. 3.9. In inset, the same in log-scale. Solid lines of SC [case (b) in blue; (c) in purple and (d) in brown] feature oscillations of the correlator, as the mark of SC. Dashed lines correspond to WC [case (a) in green and (e) in blue]. Note that although the blue dashed line (e) appears to be similar to other SC lines, it does not oscillate in the log-scale, where it only features a single local minimum. In the same way, the brown line (d) that seems not to oscillate actually features an infinite set of local minima, as is revealed in the log scale.
$\includegraphics[width=0.66\linewidth]{chap3/fig8-CorrelatorSS-and-log-for-Points-on-pyr.eps}$

Figure 3.8 shows the $\tau$ dynamics in the SS (when the dynamics has converged and is steady), for five cases of interest to be discussed later (in Fig. 3.9). A first look at the dynamics would seem to gather together a group of two curves that decay exponentially to good approximation (and remain positive as a result), and another group of three that assume a local minimum. The correct classification is the most counter-intuitive in this regard, as it puts together the dashed lines on the one hand and the solid on the other. The mathematical reason for this classification is revealed in the inset, where the same dynamics is plotted in log-scale. The dashed (resp. solid) lines correspond to parameters where the system is in WC (resp. SC) according to the definition, i.e., to values of that are imaginary on the one hand and real on the other. In log-scale, this corresponds respectively to a damping of the correlator, against oscillations with an infinite number of local minima. Note that the blue dashed line features one local minimum, which does not correspond to an oscillatory--or coherent-exchange--behavior of the fields, but rather to a jolt in the damping. These considerations that may appear abstract at this level will later turn out to show up as the actual emergence of split (dressed) states or not in the emitted spectrum.

We now return to the general (SE/SS) expression for the spectra, Eq. (3.37), that, at resonance in SC, simplifies to:

$\displaystyle S_0(\omega)=\frac{1}{2}(\mathcal{L}_\mathrm{s}^1+\mathcal{L}_\mat... ...\Im\{D_0\}-\Gamma_{-}}{2R_0}(\mathcal{A}_\mathrm{s}^1-\mathcal{A}_\mathrm{s}^1)$

(3.51)

where we used the definition for the (half) Rabi frequency at resonance, Eq. (3.33), and

$\begin{subequations}\begin{align}\mathcal{L}_\mathrm{s}^{\substack{1,2}}(\omega)... ...ac{\omega\pm R_0}{\Gamma_+^2+(\omega\pm R_0)^2}\,. \end{align}\end{subequations}$

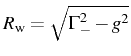In the weak coupling regime, with pure imaginary ( $g<\vert\Gamma_-\vert$ ), the positions of the two peaks collapse onto the center, $\omega_a=\omega_b=0$ . Defining $iR_\mathrm{w}=R_0$ , with $R_\mathrm{w}=\sqrt{\Gamma_-^2-g^2}$ a real number, the general expression for the spectra rewrites as:

$\displaystyle S_0^\mathrm{w}(\omega)$	$\displaystyle =\left(\frac{1}{2}+ \frac{\Gamma_--g\Im\{D_0\}}{2R_\mathrm{w}}\right)\mathcal{L}_\mathrm{w}^1$
	$\displaystyle +\left(\frac{1}{2}-\frac{\Gamma_--g\Im\{D_0\}}{2R_\mathrm{w}}\right) \mathcal{L}_\mathrm{w}^2$
	$\displaystyle -\frac{g\Re\{D_0\}}{2 R_\mathrm{w}}(\mathcal{A}_\mathrm{w}^1-\mathcal{A}_\mathrm{w}^2)\,,$	(3.53)

with the Lorentzian and dispersive contributions now given by:

$\begin{subequations}\begin{align}\mathcal{L}_\mathrm{w}^{\substack{1,2}}(\omega)... ...{\omega}{(\Gamma_+\pm R_\mathrm{w})^2+\omega^2}\,. \end{align}\end{subequations}$

Before addressing the specifics of the SE and SS cases, it is important to note that, at resonance, the Lorentzian and dispersive parts [Eqs. (3.55) and (3.57)] are invariant under the exchange of indexes $a\leftrightarrow b$ . This is simply because $\Gamma_+$ and are invariant under such transformation. Therefore, the photon and the exciton spectrum are composed of the same lineshapes, differing in the prefactor that weights them in Eq. (3.54).

Subsections