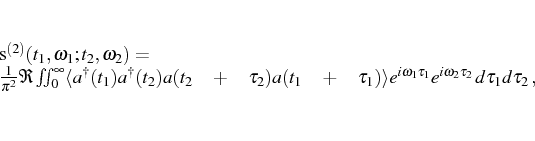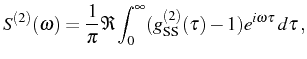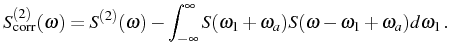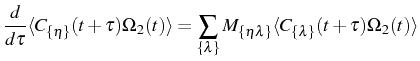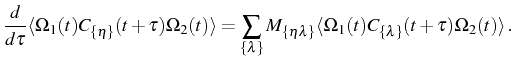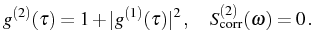Second order correlation function and the noise spectrum
The power spectrum can only provide information on probabilities for
single particles, being the Fourier transform of the first-order
correlation function
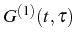 . To investigate the statistics,
we must go further in the order of the correlation functions. We
already discussed the degree of second order coherence of a
distribution,
. To investigate the statistics,
we must go further in the order of the correlation functions. We
already discussed the degree of second order coherence of a
distribution, 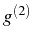 , in Eq. (2.7). Now
we can generalize it to an arbitrary delay and define the two-time
second-order correlation function:
, in Eq. (2.7). Now
we can generalize it to an arbitrary delay and define the two-time
second-order correlation function:
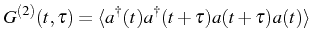 |
(2.109) |
and its normalized version for stationary states,
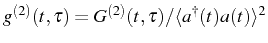
.
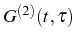
is related to the probability to emit two particles one after the
other, at times
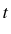
and
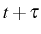
, and it can also be identified with
intensity correlations. Let us from now on consider that
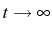
and write expressions for the SS only, as this will be the
most relevant case. As in the time domain, in order to fully describe
the correlations between two particles emitted at different
frequencies
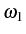
,
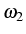
, one would have to compute
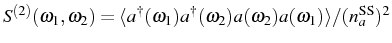
. Even
more interesting is the two-photon counting resolved in frequency,
which is related to a double Fourier transform
in the SS (
). This is linked to the probability to detect the
first photon at
with frequency
and the second, at
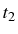
with frequency
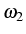
. It is possible to obtain
experimentally, integrating over some time and frequency windows, but
quite technically involved in theory, as it requires at least
three-time correlators (three implementations of the QRF). Therefore,
we leave this for future investigations and, as a first approximation
to the problem, we will simply analyze
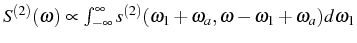
. It
corresponds to the Fourier transform
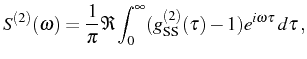 |
(2.110) |
so it can be considered the intensity fluctuation spectrum or
noise spectrum, in analogy with the power
spectrum.
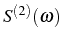
can also be interpreted as the joint
density of probability that two particles in the system have
frequencies whose fluctuations around the bare reference frequency
(
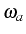
) sum up to
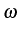
. Still working with this simplified
version of
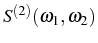
, the two-particle frequency
correlations are to be found in the difference between
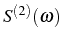
and the convolution of individual densities of
probability:
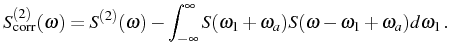 |
(2.111) |
The correlator
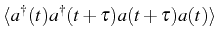 needed
here, can again be computed thanks to the QRF in the following
way. Once Eq. (2.98) is satisfied for some
set of operators
needed
here, can again be computed thanks to the QRF in the following
way. Once Eq. (2.98) is satisfied for some
set of operators
 , not only
Eq. (2.99) holds, but also the relation
, not only
Eq. (2.99) holds, but also the relation
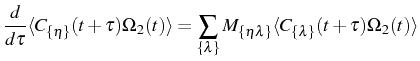 |
(2.112) |
is true for any general operator
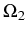
, with the same regression
matrix. From this, another useful equation involving two operators can
be derived:
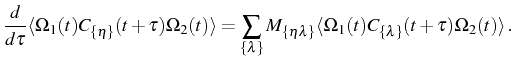 |
(2.113) |
In the present case, we need to take
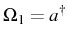
and
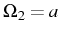
, and find the set
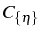
that includes the
operator
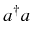
. It is interesting to note that the matrix of
regression
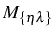
and the set of correlators
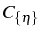
involved in the computation of
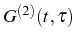
are
the same as those involved in the computation of the one-time average
value
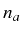
.
For the simple example of a thermal bosonic field, only the operators
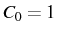 and
and
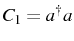 are needed with
are needed with
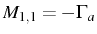 and
and
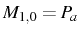 . The result in the SS is
. The result in the SS is
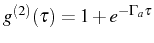 , that decays from
, that decays from 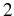 (as it
corresponds to the thermal SS) to the general infinite delay value of
(as it
corresponds to the thermal SS) to the general infinite delay value of
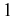 (two uncorrelated emissions). Thermal or chaotic sources
correspond to the case where each emission event is independent and:
(two uncorrelated emissions). Thermal or chaotic sources
correspond to the case where each emission event is independent and:
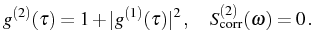 |
(2.114) |
Elena del Valle
©2009-2010-2011-2012.
![]() . To investigate the statistics,
we must go further in the order of the correlation functions. We
already discussed the degree of second order coherence of a
distribution,
. To investigate the statistics,
we must go further in the order of the correlation functions. We
already discussed the degree of second order coherence of a
distribution, ![]() , in Eq. (2.7). Now
we can generalize it to an arbitrary delay and define the two-time
second-order correlation function:
, in Eq. (2.7). Now
we can generalize it to an arbitrary delay and define the two-time
second-order correlation function:
![]() needed
here, can again be computed thanks to the QRF in the following
way. Once Eq. (2.98) is satisfied for some
set of operators
needed
here, can again be computed thanks to the QRF in the following
way. Once Eq. (2.98) is satisfied for some
set of operators
![]() , not only
Eq. (2.99) holds, but also the relation
, not only
Eq. (2.99) holds, but also the relation
![]() and
and
![]() are needed with
are needed with
![]() and
and
![]() . The result in the SS is
. The result in the SS is
![]() , that decays from
, that decays from ![]() (as it
corresponds to the thermal SS) to the general infinite delay value of
(as it
corresponds to the thermal SS) to the general infinite delay value of
![]() (two uncorrelated emissions). Thermal or chaotic sources
correspond to the case where each emission event is independent and:
(two uncorrelated emissions). Thermal or chaotic sources
correspond to the case where each emission event is independent and: