Complex potentials.
(Lecture 9 of Mathematical Methods II.)
Potential theory studies functions $\Phi$ that satisfy Laplace's equation~$\nabla^2\Phi=0$, that is, it is the theory of harmonic functions. The name arises from the historical realization that vector fields—those that arose from physical models of the world—can be described by simpler scalar fields, namely, potentials, whose gradient fully specify the physical object. For instance, in electrostatics, the vector field is the electric one, $\mathbf{E}$, to which a charge $q$ is subject through the force $\mathbf{F}=q\mathbf{E}$ it experiences. The electric potential $\Phi$ provides $\mathbf{E}=-\nabla\Phi$. In a space devoid of charge ($\rho=0$), Gauss's law $\nabla\cdot\mathbf{E}=\rho/\epsilon$ leads to $\nabla\cdot(\nabla\Phi)=0$, which is Laplace's equation. Other examples could be given with temperature fields, gravity, etc. We will mention below the case of electricity again and of fluids.
In two dimensions, one can take advantage of the powerful complex calculus to manipulate such functions through their tight link to holomorphic functions: for such a $\Phi$, there exists $F$ holomorphic such that $F(z)=\Phi(x,y)+i\Psi(x,y)$ with $\Psi$ also harmonic. The function $F$ is called the complex potential of $\Phi$. $\Psi$ has the physical meaning of lines of forces, since the curves $\Psi(x,y)=\mathrm{cst}$ are orthogonal to the equi-potential lines $\Phi(x,y)=\mathrm{cst}$.
We will first solve a simple problem in the conventional way of imposing its geometry and finding the solution. The basic case is the potential between two infinite parallel plates situated on the $x$ axis at $\alpha$ and $\beta$ and with applied potential $\Phi_\alpha$ and $\Phi_\beta$. The potential $\Phi$ is $y$ independent by symmetry, and integrating twice the equation $\Phi''=0$ we arrive to $\Phi(x)=\alpha x+\beta$, with $\alpha$, $\beta$ some constants to be determined by the boundary conditions we have imposed. This is the real part of the complex potential. The harmonic conjugate is easily found through the Cauchy-Riemann conditions, $\partial_y\Psi(y)=\partial_x\Phi(x)=\alpha$. The complex potential $\Phi(x)+i\Psi(y)=\alpha(x+iy)+\beta$ and since $x+iy=z$, (also spelling out the integration constants), we find the complex potential of the two plates facing each other:
\begin{equation} F(z)=\left(\frac{\Phi_\alpha-\Phi_\beta}{\alpha-\beta}+\frac{\Phi_\alpha-\Phi_\beta}{\alpha-\beta}\right)z+\frac{1}{2}\left((\Phi_\alpha+\Phi_\beta)-(\Phi_\alpha-\Phi_\beta)\frac{\alpha+\beta}{\alpha-\beta}\right)\,. \end{equation}
Most complication in this formula comes from the boundary conditions that fix the numerical values of the field. The potential itself is conceptually trivial: $F(z)=\alpha z+\beta$.
The equipotentials (real part of $F$) are lines horizontal to the plates, $x=\mathrm{cst}$, while lines of forces (imaginary part of $F$) are those perpendicular, joining the plates, $y=\mathrm{cst}$.
The same case as above but in polar representation describes the case of two cylindrical concentric plates. The Laplacian in such coordinates reads:
\begin{equation} \nabla^2\Phi=\frac{\partial^2\Phi}{\partial r^2}+\frac{1}{r}\frac{\partial{\Phi}}{\partial{r}}+\frac{1}{r^2}\frac{\partial^2{\Phi}}{\partial\theta^2}\,. \end{equation}
leading, again by symmetry, to solving the ordinary differential equation $\Phi''+\Phi'/r=0$, i.e., $\Phi''/\Phi'=-1/r$. Integrating twice, we arrive to $\Phi(r)=\alpha\ln(r)+\beta$. This being the real part of the complex potential we're looking for, we note that, since $\ln(z)=\ln(r)+i\theta$ (from $z=re^{i\theta}$), the imaginary part is precisly the argument of $z$. We could also obtain this result from the Cauchy-Riemann condition in polar coordinates, $(\partial f/\partial r)=(1/ir)(\partial f/\partial\theta)$. In any case, the complex potential for two concentric cylinders reads, also adjusting for boundary conditions:
\begin{equation} F(z)=\frac{\Phi_\alpha-\Phi_\beta}{\ln(r_\alpha-r_\beta)}\ln(z)+\frac12\frac{\Phi_\alpha+\Phi_\beta}{\Phi_\alpha-\Phi_\beta}\frac{\ln(r_\alpha r_\beta)}{\ln(r_\alpha/r_\beta)}\,. \end{equation}
This time, equipotentials are $r=\mathrm{cst}$, circles enclosed by the cylinders and lines of forces $\theta=\mathrm{cst}$ the perpendiculars joining them. As it should, on physical grounds.
A strength of potential theory is that any linear superposition of solutions is also a solution. The complex potential of one line charge at point $z_0$ being, as we have just seen, the complex logarithm $F_1(z)=\alpha\ln(z-z_0)$, that for two such lines, say of opposite charges $\alpha$ and at $z_0$ and $-z_0$, reads:
\begin{equation} \tag{1} F(z)=\alpha[\ln(z-z_0)-\ln(z+z_0)]\,. \end{equation}
The equipotentials are then $\mathrm{Re}(F(z))=\mathrm{cst}$, i.e.,
\begin{equation} \left|\frac{z-z_0}{z+z_0}\right|=\mathrm{cst} \end{equation}
seeing the argument of the log $Z=\frac{z-z_0}{z+z_0}$ as a complex number $Z=Re^{i\Theta}$, we have, again, $\ln(Z)=\ln R+i\Theta$ with $R=|Z|$; its log is constant when it is itself constant, resulting in the above equation. By the same argument, the lines of forces follow from $\mathrm{Im}(F)=\arg\frac{z-z_0}{z+z_0}=\mathrm{cst}$, which reduces to $\theta_1-\theta_2=\mathrm{cst}$. Both conditions are those for circles. It is straightforward by substitution $x+iy$ for the equipotentials. For the imaginary part, the reasoning is slightly more involved. The complex numbers $z-z_0$ and $z+z_0=z-(-z_0)$ define the segments joining $z$ and $\pm z_0$, the arguments of which are shown as $\theta_1$ and $\theta_2$ in the figure below. By elementary trigonometry, one can relate the difference of argument to the angle subtended by the segment $(-z_0,z_0)$.
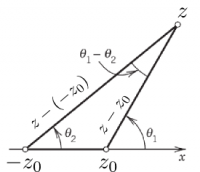
The condition defining the lines of forces of the complex potential of two charges, $\mathrm{Im}(F)=\theta_1-\theta_2=\mathrm{cst}$, is the condition for a circle that passes by the points $-z_0$, $z$ and $z_0$.
The condition for a fixed angle is for the point to describe a circle passing by these points, achieving the demonstration. The equipotentials (solid) and lines of force (dashed) are plotted below (the charges are the two white disks):
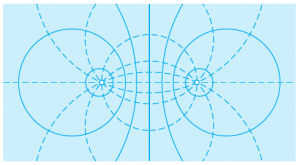
Note that the lines of the complex potential, both the equipotentials (real part) and the lines of force (imaginary) are exact circles, in contrast to the dipole in 3D.
Once that we have the potential, we can accommodate various physical configurations to it. An equipotential can be enforced by placing a solid with a charge distribution there. The solutions we have just obtained, for instance, would describe the field distributions for the two following geometries, where we matched some interesting potential solutions with those established by some objects with the ad hoc shapes:
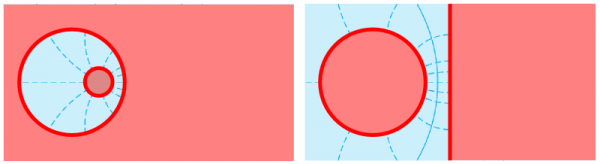
This shows the opposite approach to potentials than the one we started with, having a geometry and finding the potential. We can pick any potential we like (that is, an holomorphic function), combine it with one other or more potentials, obtain the equipotentials from the real part and lines of forces from the imaginary part, and attach a physical problem to them.
We will illustrate this approach with an irrotational fluid, in which case its field of velocity can be derived from a potential:
\begin{equation} V_x=\frac{\partial\Phi}{\partial x}\,,\quad V_y=\frac{\partial\Phi}{\partial y}\,. \end{equation}
If furthermore the fluid is incompressible, it satisfies Laplace's equation. The holomorphic $F(z)=\Phi+i\Psi$ provides (from $F'(z)=\partial_x\Phi+i\partial_y\Psi=\partial_x\Phi-i\partial_y\Phi$) the complex velocity as:
\begin{equation} V_x+iV_y=F'(z)^*\,. \end{equation}
The speed at a given point is $|F'(z)|$. Points where $F'(z)=0$ are stationary points, where the fluid doesn't move. The imaginary part of the complex velocity is the more meaningful, as it describes streamlines of the flow.
Let us now proceed with our approach of exploring complex potentials. We derived already $z$ and $\ln(z)$ from physical examples. Let us assume $F(z)=z^2$. This can be used to describe a flow past a corner, since $\mathrm{Im}(z^2)=2xy$ has solution $x=0$ and $y=0$ (when equated to zero). If we choose another streamline as another boundary condition—and it can be any of them that makes physical sense—we describe the flow of a stationary (irrotational, incompressible) fluid in the confine shown below, in red, in which case the streamlines outside the region of physical interest can be discarded (they are plotted in gray dashed lines):
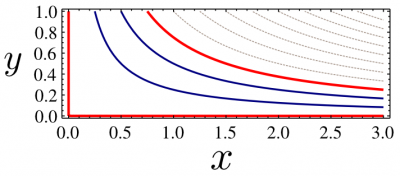
Streamlines of the complex potential $F(z)=z^2$. This can be interpreted as describing the flow past a corner, further constrained by one of the streamline $xy=\mathrm{cste}$ as shown here; any one of them is a valid boundary condition.
The potential
\begin{equation} F(z)=z+\frac1{z}\,. \end{equation}
yields, passing by the polar form, $F=(r+\frac1r)\cos\theta+i(r-\frac1r)\sin\theta$, streamlines as:
\begin{equation} \left(r-\frac1r\right)\sin\theta=\mathrm{cst} \end{equation}
with at least two obvious solutions, $r-1/r=0$ and $\sin\theta=0$, yielding the unit circle and the real axis. The general solutions, for $\mathrm{cst}\neq0$, are easily obtained with a computer, and are shown in the figure below:
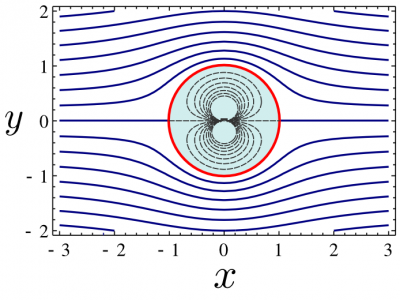
Streamlines of the complex potential $F(z)=z+\frac1{z}$. This describes the flow of the fluid past a cylinder (a circle in its 2D cross section).
This describes the important problem of a flow past a cylinder, in which case, we can discard streamlines inside the circle, shown above in dashed gray lines. Next, we will motivate conformal mapping as a way to take advantage of such particular potential solutions.
